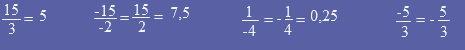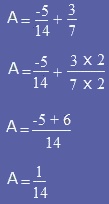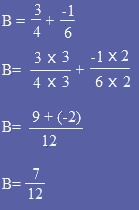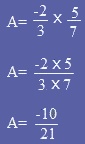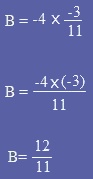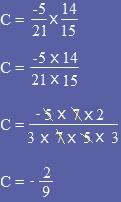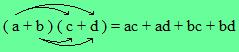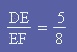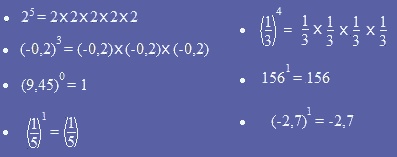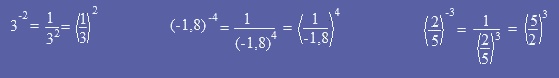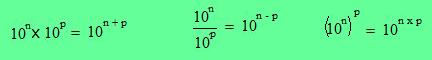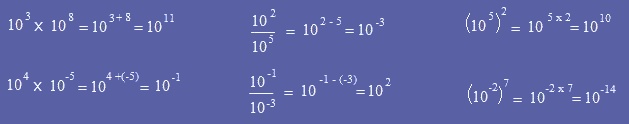|
|
 |
Bonjour, moi c'est profznic, vous
trouverez les cours de quatrième sur cette page.
Le but de ce site
est uniquement de vous présenter un cours, et de vous donner
des exercices écrits.
Si vous cherchez
un site d'exercices en ligne, avec corrigés et aide je vous
conseille Math
En Poche, qui est ce qui se fait de mieux en la matière.
Enfin, si jamais
vous avez des remarques, n'hésitez pas... |
 |
|
| |
| Commençons par le programme : (lien vers les instructions
officielles) |
| |
Activité
numérique |
Activité
géométrique |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| Et Maintenant les cours
: |
remarque :
Les cours seront toujours construits
suivant le même plan : le cours au centre et des commentaires
sur les côtés, les commentaires ne sont pas primordiaux,
mais ils permettent une meilleure compréhension. Vous trouverez
aussi des liens en fin de chapitre vers des exercices en relation
avec le chapitre.
|
| |
|
Les nombres relatifs |
| |
|
|
| |
Remarque :
-
Dans la plupart des chapitres concernant des règles de calculs, les propriétés sont franchement indigestes, le plus important n'est donc pas de retenir par coeur cette propriété, mais de la comprendre grâce aux exemples qui suivent.
- Tous les calculs doivent être écrits en colonnes pour faciliter la lecture des signes et éviter le plus possible les erreurs.
|
| |
I - Addition et soustraction de nombres relatifs (rappel de 5ème) |
|
| |
a) addition de deux nombres relatifs
|
|
| |
Propriété :
- La somme de deux nombres relatifs de même signe est le nombre :
- dont le signe est le signe commun aux deux membres ;
- dont la distance à zéro est la somme des distances à zéro des deux nombres.
- La somme de deux nombres relatifs de signes contraires est le nombre :
- dont le signe est celui du nombre ayant la plus grande distance à zéro ;
- dont la distance à zéro est la différence entre la plus grande et la plus petite distance à zéro.
|
|
Cette propriété est ce qui se fait de pire au collège,
pour bien réussir ce genre de calcul, la meilleur méthode reste celle de l'ascenseur,
un nombre positif est un nombre d'étage montée et un négatif , un nombre d'étage descendue...
le résultat est l'étage auquel vous arrivez. |
| |
Remarque : écrit comme ça, du premier coup on comprend pas grand chose, mais je vous avez prévenu.... |
| |
Exemple :
| (+9) + (+8) = +17 |
(-9) + (-8) = -17 |
(+9) + (-8) = +1 |
(-9) + (+8) = -1 |
|
| |
Propriété :
La somme de deux nombres relatifs opposés est égale à 0
|
|
Autrement dit : montez et descendez de la même chose et vous n'aurez pas bougé |
| |
 |
Notation : l'opposé d'un nombre relatif "a" est noté : "-a". |
Exemples :
(+5) + (-5) = 0
|
(-28) + (+28) = 0 |
|
|
|
| |
|
|
| |
b) soustraction de deux nombres relatifs
|
|
| |
Propriété :
Soustraire un nombre relatif revient à ajouter son opposé, ce qui se traduit par :
a et b étant deux nombres relatifs, a - b = a + (-b)
|
|
Cette propriété toute simple est en fait très importante,
elle vous dit qu'on peut passer facilement d'une addition à une soustraction.
Pour cela il suffit de changer le signe du nombre considéré,
ce sera particulièrement utile pour le paragraphe suivant. |
| |
Exemples :
| (+9) - (+8) = (+9) + (-8) = +1 |
(-9) - (-8) = (-9) + (+8) = -1 |
|
|
| (+9) - (-8) = (+9) + (+8) = +17 |
(-9) - (+8) = (-9) + (-8) = -17 |
|
|
|
| |
c) somme algébrique
|
|
| |

|
Propriété :
- Un nombre relatif positif peut être écrit sans le signe + et sans parenthèses
- dans une somme algébrique, les parenthèses peuvent être supprimées autour du premier nombre et autour d'un nombre relatif positif noté sans le signe +
|
|
|
| |
|
|
| |
Enoncé : Effectuer le calcul suivant : A = (-5) + (+4) + (-3) - (+7) + (-6) - (-9) |
|
| |
|
|
| |
Correction :
| A = (-5) + (+4) + (-3) - (+7) + (-6) - (-9) |
1) on écrit l'expression avec uniquement des nombres positifs (grâce à la propriété précédente) |
| A = -5 + (+4) - (+3) - (+7) - (+6) + (+9) |
2) on supprime les parenthèses et les signes + |
A = -5 + 4 - 3 - 7 - 6 + 9 |
3) on regroupe les termes positifs et les termes négatifs |
A = 4 + 9 -5 -3 -7 - 6 |
4) on effectue séparement les calculs |
A = 13 - 21 |
5) on termine le calculs |
A = - 8 |
6) on conclut |
|
Cette méthode fonctionnera pour tout les calculs de nombres relatifs, son principe est simple : d'abord on simplifie l'écriture puis on effectue les calculs.
|
| |
|
|
| |
II - Multiplication de nombres relatifs |
|
| |
a) multiplication de deux nombres relatifs
|
|
| |
Règle des signes :
- le produit de deux nombres relatifs de même signe est un nombre Positif.
- le produit de deux nombres relatifs de signes contraires est un nombre Négatif.
|
|
Lorsqu'on a une multiplication à effectuer il n'y a pas tout le temps de parenthèses,
alors considérez TOUJOURS un nombre avec le signe devant lui
|
| |
Exemples :
| (+9) x (+8) = + 72 |
(-9) x (-8) = + 72 |
(-9) x (+8) = - 72 |
(+9) x (-8) = - 72 |
|
| |
remarques : cas particuliers
- le produit d'un nombre relatifs par 1 est égale à lui même.
- le produit d'un nombre relatif par -1 est égale à l'opposé de ce nombre.
- le produit d'un nombre relatif par 0 est égale à 0
ainsi, "a" étant un nombre relatif ,
|
|
| |
b) multiplication de plusieurs nombres relatifs
|
|
| |
Propriété :
- Si le nombre de facteurs Négatifs d'un produit est pair, alors ce produit est Positif.
- Si le nombre de facteurs Négatifs d'un produit est impair, alors ce produit est Négatifs.
|
|
comme pour la somme algébrique, il est important de commencer par simplifier l'écriture (ici en s'occupant du signe) puis de faire le calcul |
| |
Exemple :
Il y a quatre facteurs négatifs, or 4 est un nombre pair, donc le produit est positif. |
Il y a trois facteurs négatifs, or 3 est un impair, donc le produit est négatif. |
| -6 x (-3) x 5 x (-2) x (-4) = + 720 |
4 x (-3) x (-5) x 2 x (-10) = - 1200 |
et 6 x 3 x 5 x 2 x 4 = 720
|
et 4 x 3 x 5 x 2 x 10 = 1200 |
|
| |
|
|
| |
II - division de deux nombres relatifs |
|
| |
Rappel :
Le quotient d'un nombre relatif a par un nombre relatif b (différent de zéro) est le nombre par lequel il faut multiplier b pour obtenir a. on le note 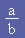
ainsi : a et b étant deux nombres relatifs, avec b  0, b x 0, b x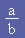 = a = a |
|
Tout ça pour dire que le quotient est le résultat d'une division et qu'on peut l'écrire sous la forme d'une fraction. |
| |
|
|
| |
Propriété :
- le quotient de deux nombres relatifs de même signe est un nombre positif.
- le quotient de deux nombres relatifs de signes contraires est un nombres négatif.
|
|
On verra dans le chapitre sur les fractions qu'on peut passer très rapidement d'une division à une multiplication, voilà pourquoi on retrouve la même règle des signes. |
| |
Exemples :
|
| |
|
|
| |
III - Priorité opératoire avec les nombres relatifs |
|
| |
Les priorités opératoires restent les même que celles vues en 5ème (multiplication et division, puis addition et soustraction), il faut cependant accentuer l'attention portée aux signes avant chaque calcul, et pour rappel :
ON CONSIDERE TOUJOURS UN NOMBRE AVEC SON SIGNE. |
|
| |
|
|
| |
Exemple : Effectuer le calcul suivant : A = 5 - (4 - 3 x (2 + 8)) |
|
| |
| A = 5 - (4 - 3 x (2 + 8)) |
1) on commence par s'occuper du calcul entre parenthèses |
| A = 5 - (4 - 3 x 10) |
2) dans les parenthèses, c'est la multiplication qui est prioritaire |
| A = 5 - (4 - 30) |
3) il reste la soustraction pour finir le calcul entre parenthèses |
| A = 5 - (-26) |
4) on simplifie l'écriture |
| A = 5 + 26 |
5) on finit le calcul |
| A = 31 |
6) on conclut |
|
Ce genre de calcul est courant le jour du brevet, mais avec des fractions.
il est donc important de bien maitriser ces priorités et de faire attention aux signes. |
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les nombres relatifs |
|
| |
| |
|
Introduction à la géométrie |
| |
Jusqu'en 5ème, les exercices de géométrie était en grande partie constitués de la même manière :
d'abord tracer un dessin, puis répondre à une question en justifiant par un théorème vu dans le cours.
On voit donc beaucoup de théorèmes très courts qui n'étaient utilisés qu'une à deux fois.
En 4ème le fonctionnement est tout autre, on ne voit que très peu de théorèmes, par contre
ils sont utilisés extremement souvent.
De plus ces théorèmes mélangent géométrie et calcul ce qui est une grande nouveauté par rapport au programme des années précédentes.
Ces théorèmes étant peu nombreux, ils vont être associés à un type de figure, il sera donc important de mettre en place des automatisme : du genre "tiens ma figure c'est un triangle rectangle, donc je dois utilisé Pythagore", ce genre d'automatisme permet de gagner du temps lorsque l'on est en devoir.
Pour bien réussir son année de 4ème, il est donc nécessaire de bien connaître
ces petits théorèmes de 5ème (qui le plus souvent sont assez évident), et de faire énormement
d'exercice sur les théorèmes de 4ème pour bien les maitriser.
|
|
| |
Pour vous aider voilà de quoi se remémorer tout ça : les indispensables en fin de 5ème |
|
| |
ainsi que des exercices :
|
révision en géométrie |
|
|
| |
|
|
|
| |
|
Le théorème de Pythagore
| |
Remarque :
- Dans toute la partie géométrie : les longueurs
n'ont rien à voir dans les hypothèses, elles permettent
certes de faire les calculs, mais elles ne servent à rien pour justifier
le théorème.
- Dans ce chapitre on utilise la racine carrée d'un nombre, pour simplifier la lecture du cours, vous trouverez une annexe traitant de la racine carrée à la fin du cours.
|
|
|
| |
I - Le théorème de Pythagore |
|
| |
Théorème :
Si un triangle est rectangle, alors le carré de son hypoténuse est égal à la somme des carrés des longueurs des côtés de l'angle droit.
|
|
Demandez à vos parents de vous le citer, je suis sur qu'ils s'en souviennent encore.... |
| |
Remarque : il ne sert à rien de retenir cette formulation, en effet, ce théorème ayant un nom, il suffira de citer ce nom. |
|
| |
Application : pour calculer une longueur :
|
|
| |
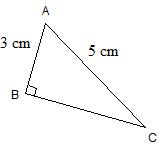
| Enoncé : |
Soit ABC un triangle rectangle en B tel que : |
 |
| |
AB = 3 cm et AC = 5cm |
| |
|
| |
Calculer la longueur BC |
|
Un triangle et 2 longueurs, c'est un cas classique d'utilisation de Pythagore, retenez bien cette figure !!!!!!!! |
| |
Correction :
|
Cette rédaction est ce qu'on attendra de vous le jour du brevet, alors autant vous appliquez à rédiger de cette façon tout de suite... |
| |
|
|
| |
II - La réciproque du théorème de Pythagore |
|
| |
On vient de voir que si un triangle est rectangle, alors on a la relation numérique avec les longueurs des côtés.
La question que l'on doit alors se poser est : celà marche-t-il dans l'autre sens, c'est à dire si j'ai un triangle quelconque qui vérifie la relation numérique, puis-je démontrer qu'il est rectangle?
La réponse est OUI, c'est celà la réciproque du théorème de Pythagore. |
|
| |
Théorème :
Si le carré de la longueur d'un côté d'un triangle est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle.
|
|
|
| |
 |
Pour utiliser ce théorème il faut d'abord faire le calcul du carré des longueurs SEPAREMENT : |
|
|
| |
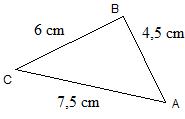
| Enoncé : |
Soit ABC un triangle tel que : |
 |
| |
AB = 4,5 cm, BC = 6 cm et AC = 7,5 cm |
| |
|
| |
Démontrer que le triangle ABC est rectangle. |
|
Un triangle et 3 longueurs, c'est un cas ultra classique d'utilisation de la réciproque de Pythagore, alors retenez bien cette figure !!!! |
| |
Correction :
|
l'erreur classique des élèves sur ce théorème et d'oublier le on sait que et de passer directement à la remarque.
Le piège favori des profs est de faire une figure dans lequel l'égalité est fausse....
Alors faites attention à
la rédaction. |
| |
|
|
| |
Annexe 1 : la racine carrée |
|
| |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec le théorème de Pythagore |
|
| |
| |
|
Les fractions |
Rappel :
Lorsqu'on effectue une division, il est rare que la résultat tombe juste, par exemple 1/3 = 0,3333333333333
pourtant, 1/3*3 =1, tandis que 0,333333333333333*3 = 0,999999999999999
on a donc un problème de précision lorsqu'on veut enchainer des calculs
Les fractions sont une solution à ce problème de précision, en effet une fraction n'est composée que de nombres entiers, malheureusement cette précision a un prix, car il faut apprendre à maitriser cette nouvelle écriture.
Une fraction n'est donc que l'écriture précise du résultat d'une division. |
| |
I - Addition et soustraction |
|
| |
a) fractions égales
|
|
| |
Propriété :
On ne change pas la valeur d'un quotient en multipliant (ou en divisant) son numérateur ET son dénominateur par un même nombre relatif non nul.
|
|
|
| |
Exemples :
|
cette propriété est très utile pour la suite. |
| |
b) addition et soustraction
|
|
| |
Règle :
Pour effectuer une addition (ou une soustraction) de deux fractions,il faut :
- qu'elles aient le même dénominateur ;
- additionner (ou soustraire) les numérateurs.
|
|
|
En fait pour additionner ou soustraire des fractions c'est comme compter des parts
de tartes,
c'est très simple de compter 1/5 + 2/5,
par contre c'est plus compliqué de compter 1/3 + 1/4,
voila pourquoi on veut avoir le même dénominateur |
| |
Méthode : pour effectuer une addition ou une soustraction, il faudra donc mettre ces deux fractions au même dénominateur en utilisant la propriété précédente. |
| |
Exemple :
|
| |
II - Multiplication |
|
| |
Règle :
Pour calculer le produit de deux fractions, on multiplie les numérateurs entre eux et les dénominateurs entre eux.
|
|
C'est l'opération la plus simple pour les fractions, on agit comme un gros barbare ....
Sauf qu'il ne faut pas oublier de simplifier le résultat à la fin du calcul et pour ça la meilleure méthode reste la décomposition de l'exemple C.
|
| |
Exemples :
|
| |
III - Division et nombres inverses |
|
| |
Définition :
on dit que deux nombres sont inverses lorsque leur produit est égale à 1
|
|
Ne pas confondre avec opposé : deux nombres sont opposés lorsque leur somme est nulle. |
| |
Exemples :
|
|
| |
|
|
| |
Exemples :
l'inverse de 4 est :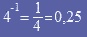 |
l'inverse de  est : est : |
|
|
|
| |
Règle :
Diviser par un nombre, c'est multiplier par son inverse
|
|
Effectuer une division est donc quelque chosede très simple, vu que l'on revient à une multiplication, il faut toutefois faire attention à la fraction que l'on inverse. |
| |
Exemples :
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les fractions |
|
| |
| |
|
Le théorème de Thalès |
| |
I - Milieux et parallèles |
|
| |
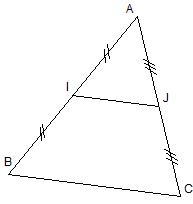
Théorème 1 :
Si une droite passe par le milieux de deux côtés d'un triangle,
Alors elle est parallèle au troisième côté.
|
|
Les trois théorèmes de ce paragraphe sont assez semblables, c'est donc la conclusion qui va vous permettre d'appliquer le bon dans un exercice |
| |
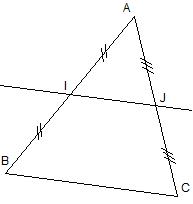
Exemple :
Soit ABC un triangle tel que :
I milieux de [AB] et J milieu de [AC]
Démontrer que (IJ) // (BC) |
 |
|
Pour bien répondre à ce genre de question, il faut d'abord réfléchir au théorème du cours qui convient, une fois celui-ci trouvé, il ne reste plus qu'à le rédiger correctement..... |
| |
Correction :
On sait que : Dans le triangle ABC
I milieu de [AB] et J milieu de [AC] |
1) on cite les données necessaire à l'application du théorème. |
Or : Si une droite passe par le milieux de deux côtés d'un triangle,
Alors elle est parallèle au troisième côté. |
2) on cite le théorème qui permet de répondre à la question |
| Donc : (IJ) // (BC) |
3) on conclut |
|
| |
Théorème 2 :
Si une droite passe par le milieu d'un côté d'un triangle et qu'elle est parallèle à un second côté
alors elle coupe le troisième côté en son milieu
|
|
Pour ces deux théorèmes, le dessin est le même que pour le premier théorème, seul les données et la conclusion vont changer. |
| |
Théorème 3 :
Si un segment a pour extrémités les milieux de deux côtés d'un triangle
Alors sa longueur est égale à la moitié de la longueur de celle du troisième côté de ce triangle
|
|
| |
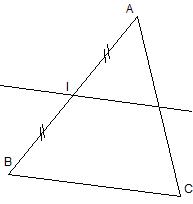
Exemple :
Soit ABC un triangle
I milieu de [AB] et (d)//(BC)
Démontrer que (d) coupe [AC] en son milieu |
 |
Soit ABC un triangle
I milieu de [AB],
J milieu ed [AC] et BC = 5 cm
Calculer IJ |
 |
|
|
| |
II - Le théorème de Thalès |
|
| |
| on sait que : |
- B appartient à (AM) |
| - C appartient à (AN) |
| - (BC) parallèle à (MN) |
| |
alors : d'après
le théorème de Thalès on
a :
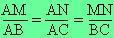
|
|
|
 |
|
La rédaction de ce
théorème étant très simple, il n'est
toléré aucune erreur dans les données et dans
le nom "Thalès". |
| |
|
|
| |
méthode
: pour calculer une longueur |
|
| |
| énoncé
: |
 |
On donne :
(BC) // (MN);
AB = 7,8 cm ; AM = 3 cm |
| MN = 7 cm
et AC = 13 cm. |
| Calculer la
longueur BC. |
|
Voici une question classique
du brevet... |
| |
|
|
| |
| correction : |
on sait que : |
1) on cite
TOUTES les données NECESSAIRE à l'utilisation
du théorème. |
| |
- M appartient à
(AB) |
| |
- N appartient à
(AC) |
| |
- (MN) // (BC) |
| |
|
|
alors d'après
le théorème de Thalès on a : 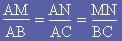 |
2) on cite le théorème
et on l'applique. |
| |
|
3) on remplace par les
valeurs. |
| |
|
4) on ne retient que ce
qui nous interesse, et on applique le produit en croix.(voir
méthode) |
| |
BC =  =
18,2 cm =
18,2 cm |
5) on finit les calculs. |
|
Rappel : les longueurs
n'ont rien à voir dans les hypothèses, elles permettent
certes de faire les calculs, mais elles ne servent à rien
pour justifier le théorème. |
| |
|
|
| |
III - Agrandissement et réduction |
|
| |
| Définition : |
- Une figure F ' est un agrandissement d'une figure F lorsque les longueurs de la figure F ' sont
|
obtenues en multipliant celles de la figure F par un même nombre "k", strictement supérieur à 1. Le nombre "k" est appelé le facteur d'aggrandisement. |
- Une figure F ' est une réduction d'une figure F lorsque les longueurs de la figure F ' sont obtenues
|
| en multipliant celles de la figure F par un même nombre "k", strictement inférieur à 1. Le nombre "k" est appelé le facteur de réduction. |
|
|
Ces définitions ont d'énormes domaines d'application dans la miniaturisation, mais elle est assez peu utilisé au collège.... |
| |
Remarque :
Dire qu'une figure F ' est un agrandissement de facteur k d'une figure F, revient à dire que la figure F est une réduction de facteur de la figure F '
|
|
| |
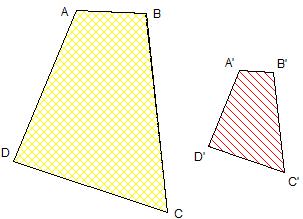
Exemple :
Les quadrilatères ABCD et A'B'C'D' sont tels que :
AB = 2 A'B' ; BC = 2 B'C' ; CD = 2 C'D' et
DA = 2 D'A'
donc le quadrilatère ABCD est un agrandissement de facteur 2 du quadrilatère A'B'C'D'
de même, le quadrilatère A'B'C'D' est une réduction de facteur  du quadrilmatère ABCD. du quadrilmatère ABCD. |
 |
|
|
| |
Propriété :
Dans un agrandissement ou une réduction, les mesures des angles et le parallélisme sont conservés. |
|
|
| |
|
|
| |
Méthode :
|
|
| |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les théorèmes des milieux et le théorème de Thalès |
|
| |
| |
|
Calcul littéral |
| |
I - Simplification de l'écriture d'un produit |
|
| |
Règles :
- Dans l'écriture d'une expression, le signe x peut être supprimé devant une lettre ou devant une parenthèse.
- Pour calculer un produit ou simplifier son écriture, on peut changer l'ordre des facteurs et les regrouper différemment.
|
|
Cette propriété vu en 5ème fonctionne surtout dans l'autre sens,
c'est à dire que lorsque vous ne voyez pas de signe entre un chiffre et un lettre : c'est une multiplication.
|
| |
Exemple :
| 3 x a = 3a |
x x y = xy |
3 x (5 + 3a) = 3(5 + 3a) |
| 4x x 3 = 4 x 3x = 12x |
2x x 5x = 2 x 5 x x x x = 10x |
|
|
| |
II - Factorisation et réduction d'une expression littérale |
|
| |
a) Factorisation
|
|
| |
Définition :
Factoriser une somme algébrique, c'est la transformer en produit
|
|
|
| |
Propriété :
a,b et k désignent trois nombres relatifs :
| ka + kb = k(a + b) |
ka - kb = k(a - b) |
|
|
La seule chose qui change est donc l'écriture de cette expression, si on remplace la lettre par un chiffre, on doit donc trouver le même résultat...
Cette propriété toute simple va toutefois vous être très utile et cela jusqu'au BAC, alors mieux vaut la maitriser... |
| |
Exemples :
| A = 3x + 6 |
B = 35y - 15y - 15y |
| A = 3 x x + 3 x 2 |
B = 5y x 7y - 5y x 3 |
| A = 3(x + 2) |
B = 5y(7y - 3) |
|
| |
b) Réduction d'une expression
|
|
| |
Définition :
Réduire une expression, c'est l'écrire avec le moins de terme possible
|
|
|
| |
Exemples :
| A = 3t - 8t |
B = -3x + 9x - 7 + 10x - 15x - 7 + 10x - 15x + 2 + 2 |
| A = (3 - 8)t |
B = 9x - 15x - 15x - 3x + 10x - 7 + 2 - 3x + 10x - 7 + 2 |
| A = -5t |
B = (9 - 15)x + (-3 + 10)x + (-7 + 2) + (-3 + 10)x + (-7 + 2) |
| |
B = -6x + 7x - 5 + 7x - 5 |
|
Une fois le truc compris, on peut passer l'étape de mise entre parenthèses et donner le résultat de suite. |
| |
III - Suppression des parenthèses |
|
| |
Propriétés :
- L'opposé d'une somme est égal à la somme des opposés de chacun de ses termes
- L'opposé d'une différence est égal à la différence des opposés de chacun de ses termes.
| c'est à dire : |
|
| |
- (a + b) = -a - b |
et - (a - b) = -a + b |
|
|
Il va donc falloir
être très attentif aux signes, car c'est la source de 90% des erreurs le jour
du brevet. |
| |
Exemples :
| - (x + 3) = -x - 3 |
- (-y - 5) = y + 5 |
|
| |
Propriétés :
a + (b + c) = a + b + c |
et |
a + (b - c) = a + b - c |
a - (b + c) = a - b - c |
et |
a - (b - c) = a - b + c |
|
|
|
| |
Exemples :
| A = 2 + (3x - 5) |
B = 6y - (2y - 16) |
| A = 2 + 3x - 5 |
B = 6y - 2y + 16 |
| A = 3x - 3 |
B = 4y + 16 |
|
|
| |
IV - Développement d'une expression littérale |
|
| |
| Définition : |
| Développer une expression littérale,
c'est l'écrire comme une somme algébrique
de termes. |
|
|
|
| |
| Propriété : soit a, b, c, d et k sont des nombres, alors on a : |
k ( a + b ) = ka + kb |
k ( a - b ) = ka - kb |
|
|
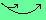 |
|
|
| |
|
|
L'exemple est choisi volontairement simple pour la compréhension.
Lors de vos premiers essais, n'hésitez pas à mettre les flèches, comme dans la propriété, et surtout ATTENTION aux SIGNES
|
| |
Exemples :
| A = (2x + 3) (5x + 4) |
| A = 2x x 5x + 2x x 4 + 3 x 5x + 3 x 4 |
A = 10x + 8x + 15x + 12 + 8x + 15x + 12 |
A = 10x + 23x + 12 + 23x + 12 |
|
| |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec le calcul littéral |
|
| |
| |
|
Triangle rectangle et trigonométrie |
|
Il important de
retenir que tout ce qui va être dit ne concerne que les triangles
rectangles. |
 |
De plus, contrairement à
d'autres outils mathématiques, la trigonométrie n'utilise
pas de théorème |
ce qui simplifie nettement
la rédaction et donc celle-ci se doit d'être parfaite. |
|
|
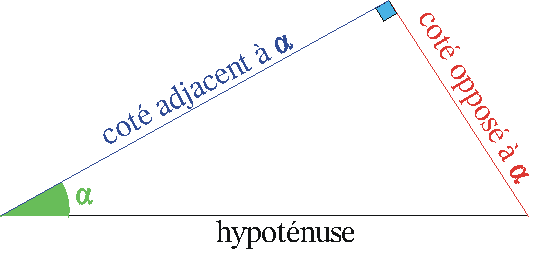
Dans un triangle rectangle, |
soit a un angle différent de l'angle droit. |
on définit
alors deux côtés par rapport à a : |
le côté adjacent
à a : c'est le côté reliant l'angle a et l'angle droit.
|
le côté opposé
à a : c'est le côté "en face" de
l'angle a
|
|
 |
|
remarque : il y a deux possiblités pour a, donc
il faut bien réfléchir à l'angle que l'on considère
avant de décider quel côté est adjacent.... |
| |
|
|
| |
| Définitions : |
Dans un triangle rectangle on a :
|
- le cosinus d'un angle aigu est égal au quotient
:
|
|
|
Cette formule est à
connaître par coeur, on va voir au second chapitre son application.
J'insiste, cette formule n'est valide QUE DANS UN TRIANGLE RECTANGLE. |
| |
|
|
| |
| Exemple : |
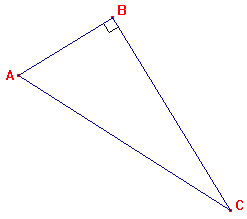 |
On sait que : ABC
est un triangle rectangle en B |
| donc : |
- 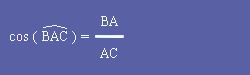 |
| |
|
| |
|
|
C'est l'étape la
plus importante lors de l'utilisation de la trigonométrie.
Il faut être capable de donner le cosinus d'un
angle sans se tromper. Je vous conseille de vous exercer sur mathenpoche avant de passer au calculs. |
| |
|
|
| |
| Propriété : |
Pour tout angle aigu a, on a : |
| |
- 0 < cos a < 1 |
|
|
Cette formule n'est pas
très importante en 4ème, Elle permet surtout de vérifier si on n'a pas écrit la relation à l'envers. |
| |
|
|
| |
II -
Applications |
|
| |
a) pour calculer une longueur
|
|
| |
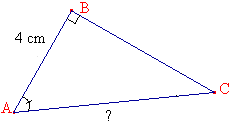
| Enoncé : |
soit ABC un triangle rectangle
en B |
 |
|
|
 |
|
tel
que AB = 4 cm et BAC = 48° |
| |
Calculer la longueur AC
au mm près. |
|
Voici un énoncé
typique d'un exercice de brevet. |
| |
Correction :
| On sait que le triangle
est rectangle en B |
1) préciser la nature
du triangle |
|
 |
|
|
donc cos (BAC) = |
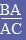 |
2) donner la
définition à l'aide de la figure |
AC = .jpg)
|
3) appliquer le produit
en croix (voir méthode) |
AC = .jpg) |
4) remplacer par les valeurs,
taper le calcul à la calculatrice |
AC = 5,98 cm
|
et donner la valeur approchée |
| AC vaut environ 6 cm |
5) conclure |
|
En fait la première
étape ici est de déterminer quel outil on va utiliser pour cela c'est la figure et la question qui doivent
vous aider.
Ici on connait le côté adjacent et on cherche l'hypothénuse......
donc c'est le cosinus. |
| |
|
|
| |
b) pour calculer
un angle
|
|
| |
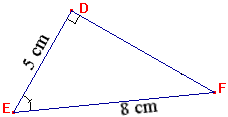
| Enoncé
: |
soit DEF un
triangle rectangle en D |
 |
|
tel
que DE = 5 cm et EF = 8 cm. |
|
|
|
Calculer la mesure de l'angle
DEF au degrès près. |
|
|
| |
|
|
|
| |
Correction :
| on sait que
le triangle DEF est rectangle en D |
1) préciser la nature
du triangle |
| |
|
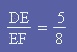 |
donc cos
(DEF) = |
|
|
2) donner la
définition à l'aide de la figure et remplacer
par les valeurs de l'énoncé |
|
|
|
| à la calculatrice
on a DEF = 51° |
3) utiliser votre calculatrice (voir
méthode) |
| |
et donner la valeur approchée |
|
Ici on connait le côté adjacent et l'hypoténuse, donc
c'est le cosinus. |
| |
|
|
| |
Les méthodes
: |
|
| |
|
|
| |
| La calculatrice et la trigonométrie : |
Lorsqu'on cherche un angle à
l'aide de la trigonométrie, on est amené
à utiliser la calculatrice. |
Certain manuel vous parle alors de invcos
(pour le cos), on on peut aussi trouver les notations cos |
| Comme les élèves de 4ème ne savent
pas ce que ces notations veulent dire vraiment.
Autant être honnête et dire comme dans l'exemple
: " à la calculatrice ". |
| |
Ceci étant mis au clair, pour utiliser la calculatrice,
il suffit alors de taper pour notre exemple : cos (5/8) (5/8) |
| |
La calculatrice vous donne le résulat,
ici 51° |
|
|
Suivant le modèle de
calculatrice, ce n'est pas la même touche, donc à vous
de trouver ....
Vérifier aussi que
vous êtes bien en degrés .... |
| |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec la trigonométrie |
|
| |
|
Les puissances |
| |
I - Puissances d'exposant entier relatif d'un nombre |
|
| |
a) Exposant entier positif
|
|
| |
Définition :
"a" étant un nombre relatif et "n" un nombre entier supérieur ou égal à 2, le produit de "n" facteurs égaux à "a" est noté 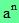

Le nombre "n" est l'exposant de a et 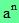 est la puissance d'exposant n du nombre a. est la puissance d'exposant n du nombre a.
De plus, a étant un nombre relatif, par convention 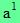 = a et = a et 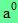 = 1. = 1.
|
|
Cette définition n'est pas nouvelle, on l'a déjà vu pour le théorème de Pythagore, elle est juste généralisée. |
| |
Remarque :  se lit " a exposant n" ou " a puissance n" ; a² se lit aussi "a au carré" et se lit " a exposant n" ou " a puissance n" ; a² se lit aussi "a au carré" et  : "a au cube". : "a au cube". |
|
| |
|
|
| |
Exemples :
|
Il faudra faire attention aux signes, mais on y revient dans le paragraphe suivant. |
| |
b) Exposant entier strictement négatif
|
|
| |
Définition :
"a" étant un nombre relatif non nul et "n" un nombre entier positif non nul, le nombre  est égal à l'inverse du nombre est égal à l'inverse du nombre 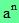
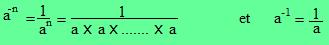
 est la puissance d'exposant -n du nombre a. est la puissance d'exposant -n du nombre a.
|
|
|
| |
Exemples :
|
|
| |
c) Signe d'une puissance d'exposant entier relatif d'un nombre
|
|
| |
Propriété :
- Une puissance d'un nombre positif est un nombre positif.
- Une puissance d'exposant pair d'un nombre négatif est un nombre positif.
- Une puissance d'exposant impair d'un nombre négatif est un nombre négatif.
|
|
Cette propriété découle directement de la règle des signes, vu dans le chapitre sur le s nombres relatifs.
En effet, à chaque fois que l'on fait des paquets de deux négatifs, on récupère un positif.
d'où l'importance de la parité.... |
| |
Exemples :
|
| |
II - Puissances de 10 |
|
| |
a) Ecriture décimale de : 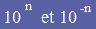
|
|
| |
Propriétés :
Pour tout entier positif "n" non nul on a :
|
|
|
| |
Exemples :
|
|
| |
b) Opérations sur les puissances
|
|
| |
Propriétés : n et p étant deux entiers relatifs et a un nombre relatif non nul, on a :
|
|
Ces formules sont à connaitre par coeur, elles sont utiles tous les ans au brevet, pour les retenir, il suffit d'écrire les prioritaires
opératoires ainsi :
et de prendre l'opération juste en dessous... |
| |
Exemples :
|
| |
Remarque : La somme et la différence de deux puissances ne sont pas des puissances, par exemple :
| 3² + 5² = 9 + 25 = 34 |
| 8² = 64 |
| il n' y a pas de simplifications possibles |
|
| |
c) Notation scientifique d'un nombre décimal non nul
|
|
| |
Définition :
La notation scientifique d'un nombre décimal non nul est la seule écriture de ce nombre sous la forme a x 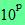 où "a" est un nombre décimal tel que 1 où "a" est un nombre décimal tel que 1 a < 10 et "p" est un entier relatif. a < 10 et "p" est un entier relatif.
|
|
Cette écriture n'est pas juste pour faire joli ou pour vous embeter, dès la seconde, dans de nombreuses matières, on l'utilise couremment. |
| |
Exemples :
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les puissances |
|
| |
|
Triangle rectangle et cercle circonscrit |
| |
I - Propriétés directes |
|
| |
a) Triangle rectangle et cercle circonscrit
|
|
| |
Propriété :
Si un triangle est rectangle,
Alors son cercle circonscrit a pour diamètre son hypoténuse.
|
|
Ce théorème n'est pas très long, et il tombe régulièrement le jour du brevet, il ne sera pas revu en 3ème, donc autant l'apprendre tout de suite .... |
| |
Remarque :
Si le diamètre est l'hypoténuse, ça veut dire que le centre du cercle est le milieu de l'hypoténuse..... |
|
| |
Exemple : |
|
| |
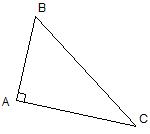
Soit ABC un triangle rectangle en A
Tracer son cercle circonscrit. |
 |
|
|
| |
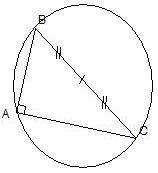
Correction :
| Le triangle ABC est rectangle en A, donc son cercle circonscrit a pour diamètre son hypoténuse [BC] |
|
|
 |
|
Cette justification est obligatoire lors du brevet et vaut plus de point que le dessin... |
| |
b) Triangle rectangle et médiane
|
|
| |
Propriété :
Si un triangle est rectangle,
Alors la médiane relative à son hypoténuse a pour longueur la moitié de celle de l'hypoténuse.
|
|
|
| |
Exemple : |
|
| |
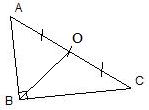
Soit ABC un triangle rectangle en B
tel que AC = 8 cm et O le milieu de [AC]
Calculer la longueur BO |
 |
|
|
| |
|
|
| |
Correction :
On sait que : ABC est rectangle en B
et O milieu de [AC] |
1) rappeler les données qui permettent de citer le théorème |
Or : Si un triangle est rectangle
Alors la médiane relative à son hypoténuse à pour longueur la moitié de celle de l'hypoténuse. |
2) citer le théorème qui va vous permettre de trouver la solution |
| Donc : BO = AC : 2 = 4 cm |
3) conclure |
|
Je rappelle que la réponse à iune question de géométrie doit toujours se présenter sous cette forme... |
| |
II - Propriétés réciproques |
|
| |
 |
Propriété :
Si un triangle est inscrit dans un cercle ayant pour diamètre l'un de ses côtés,
Alors ce triangle est rectangle et son hypoténuse est ce côté.
|
|
|
Voilà la propriété la plus importante du chapitre, à connaitre par coeur
Son utilisation n'est pas compliquée, dès que vous voyez un triangle dans un cercle, c'est celle-là. |
| |
Exemple : |
| |
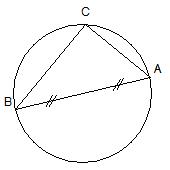
Soit (C) un cercle de diamètre [AB]
et C un point de ce cercle.
Démontrer que ABC est rectangle. |
 |
|
| |
|
|
| |
Correction :
| On sait que : Le triangle ABC est inscrit dans le cercle de diamètre [AB] |
1) rappeler les données qui permettent de citer le théorème |
Or :Si un triangle est inscrit dans un cercle ayant pour diamètre l'un de ses côtés,
Alors ce triangle est rectangle et son hypoténuse est ce côté. |
2) citer le théorème qui va vous permettre de trouver la solution |
| Donc : ABC est rectangle en C |
3) conclure |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les triangles rectangles et leurs cercles circonscrits |
|
| |
|
Equation et résolution de problèmes |
| |
I - Egalité et opérations |
|
| |
Propriété :
Lorsqu'on ajoute ou lorsqu'on retranche un même nombre aux deux membres d'une égalité, on obtient une nouvelle égalité.
a, b et c étant trois nombres relatifs, on a :
si a = b,
alors a + c = b + c et a - c = b - c |
|
|
Ces règles sont assez évidentes à comprendre (en prenant l'image d'une balance)
si on rajoute la même chose des deux cotés, la balance reste en équilibre |
| |
Exemples :
x étant un nombre relatif,
|
- si x = 8, alors x + 5 = 8 +5 et donc x + 5 = 13
|
- si x = -6, alors x - 1 = -6 - 1 et donc x - 1 = -7
|
|
Ces propriétés très simples vont être très utiles lors de la résolution d'une équation
Toutefois on les utilisera dans le sens contraire des exemples.
C'est à dire qu'on ne cherchera pas à rajouter un nombre à "x" mais à l'enlever pour ne plus avoir que le "x". |
| |
Propriété :
Lorsqu'on multiplie chaque membre d'une égalité par un même nombre, on obtient une nouvelle égalité.
a, b et c étant trois nombres relatifs, on a :
si a = b, alors a x c = b x c |
|
|
| |
Exemple :
x étant un nombre relatif,
si x = -3, alors x x 4 = -3 x 4 et donc 4x = -12 |
|
| |
Propriété :
Lorsqu'on divise chaque membre d'une égalité par un même nombre non nul, on obtient une nouvelle égalité.
a, b et c étant trois nombres relatifs, on a :
si a = b et c 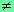 0, alors |
a |
= |
b |
c |
c |
|
|
|
|
| |
Exemple :
x étant un nombre relatif,
| si x = 10, alors |
x |
= |
10 |
donc |
x |
= |
5 |
| 2 |
2 |
2 |
|
|
|
| |
II - Equations : |
|
| |
a) généralités
|
|
| |
Définition :
Une équation est une égalité dans laquelle figure un nombre inconnu, désigné en général par une lettre appelé l'inconnue.
Une valeur de ce nombre pour laquelle l'égalité est vraie est une solution de l'équation.
|
|
|
| |
Exemples :
- 2x - 11 = 7 - x est une solution dans laquelle l'inconnue est désignée par "x".
|
2x - 11 = 7 - x |
|
2x - 11 est appelé le
premier
membre de l'équation |
7 - x est appelé le deuxième
membre de l'équation |
|
|
Ces notions ont normalement déjà été vu en 5ème,
Le plus important est de se dire que x peut être n'importe quel nombre,
Pourtant l'égalité n'est pas vrai pour n'importe quel nombre, à nous de trouver les bons "x" |
| |
- Le nombre 6 est une solution de l'équation 2x - 11 = 7 - x
|
| en effet : |
2 x 6 - 11 = 12 - 11 = 1 |
On obtient le même résultat, donc l'égalité
2x - 11 = 7 - x est vraie pour x = 6 |
|
| 7 - 6 = 1 |
|
| |
- Le nombre 3 n'est pas une solution de l'équation 2x - 11 = 7 - x
|
| en effet : |
2 x 3 - 11 = 6 - 11 = -5 |
On n'obtient pas le même résultat, donc l'égalité
2x - 11 = 7 - x est vraie pour x = 6 |
|
| 7 - 3 = 4 |
|
|
| |
Définition :
Résoudre une équation, c'est trouver toutes ses solutions.
|
|
On insiste sur le toutes dès la 3ème |
| |
b) Equations de référence
|
|
| |
|
L'équation a + x = b admet une seule solution :
x = b - a |
|
|
L'équation a x = b admet une seule solution :
|
|
| Exemples : |
|
On veut résoudre l'équation : 3 + x = -7
3 + x = -7
x = -7 - 3
x = -10 |
|
On veut résoudre l'équation -5x = 3
|
|
Pour résoudre une équation, il faudra donc toujours se ramener à l'une de ces deux formes...
On voit comment dans l'exemple suivant.
|
| |
c) Règles pour résoudre une équation
|
|
| |
Règles :
- Lorsque l'on ajoute ou que l'on retranche un même nombre aux deux membres d'une équation,
on obtient une équation qui a les mêmes solution.
-
Lorsque l'on multiplie ou que l'on divise par un même nombre non nul les deux membres d'une équation,
on obtient une équation qui a les mêmes solutions.
|
|
|
| |
Exemple : |
|
| |
| Résoudre l'équation 7x - 2 = 6 + 5x |
7x - 2 = 6 + 5x |
Le but étant de trouver x, on va commencer par mettre tous les termes en x d'un côté et les termes sans x de l'autre côté.
Pour cela, on utilise la 1ère Règle. |
7x - 2 + 2 = 6 + 5x + 2 |
|
7x - 5x = 5x + 8 - 5x |
2x = 8 |
Une fois les termes en x d'un côté et les termes sans x de l'autre, il n'y a plus qu'à appliquer la 2nde règle. |
|
x = 4 |
|
| La solution de l'équation 7x - 2 = 6 + 5x est le nombre 4. |
|
Voilà une équation classique du brevet. |
| |
III - Mettre en équation un problème pour le résoudre |
|
| |
Enoncé : Benoît a 14 ans et son père a 40 ans
Dans combien d'années l'âge du père sera-t-il le double de l'âge de Benoît ? |
|
|
| |
Solution :
| Méthode : Pour résoudre un problème, on suit cette démarche en 4 étapes : |
| 1) on choisit l'inconnue (on lit la question) |
|
| 2) on met le problème en équation (on traduit l'énoncé pour obtenir des égalités) |
| 3) on résout l'équation obtenue. |
|
| 4) on conclut en répondant à la question |
|
|
|
Cette méthode fonctionne pour tous les problèmes, le plus dur reste de l'appliquer et surtout de bien traduire l'énoncé. |
| |
| Soit x le nombre d'années cherchées |
1) on a juste repris la question |
| |
|
Dans "x" années l'âge de Benoît sera : 14 + x |
2) on a traduit l'énoncé |
et l'âge de son père sera 40 + x
|
| le double de l'âge de Benoît est : 2 x (14 + x) |
| on a donc l'équation : 2(14 + x) = 40 + x |
| |
|
| il reste à résoudre : 2(14 + x) = 40 + x |
3) on résoud l'équation |
2(14 + x) = |
|
40 + x |
28 +2x = |
|
40 + x |
28 + 2x - x = |
|
40 + x - x |
28 + x = |
|
40 |
28 + x - 28 = |
|
40 - 28 |
x = |
|
12 |
|
grâce aux chapitres précédents. |
| Le père de Benoît aura le double de l'âge de Benoît dans 12 ans. |
4) on conclut |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les équations et la résolution de problèmes |
|
| |
|
Distances |
| |
I - distances d'un point à une droite |
|
| |
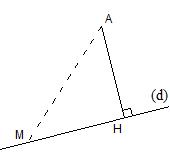
Propriété :
Soit une droite (d) et un point A n'appartenant pas à la droite (d)
- Le point de la droite (d) le plus proche du point A est le point H, pied ed la perpendiculaire à la droite (d) passant par le point A.
- La distance AH est appelée la distance du point A à la droite (d).
|
|
Cette définition vous dit juste que si vous voulez connaître la distance d'un point à une droite, vous devez tracer la perpendiculaire à cette droite passant par ce point.
Elle dit aussi que si vous reliez A avec un autre point de la droite, la distance sera plus grande.
|
| |
Exemple :
|
| La distance de A à la droite (d) est AH, et pour tout point M appartenant à (d), AH < AM |
|
| |
Cas particulier :
Lorsque le point A appartient à la droite (d),
la distance de A à (d) est nulle. |
 |
|
| |
II - Tangente à un cercle |
|
| |
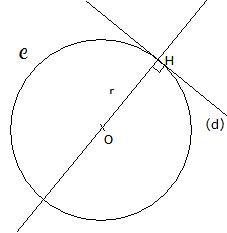
Définition :
Soit un cercle C de centre O et un point H appartenant au cercle C.
La tangente en H au cercle C est la droite passant par le point H et perpendiculaire à la
droite (OH).
|
|
Dans certain manuel, on peut trouver la définition à la place de la propriété et vice-versa,
ce n'est pas un problème, les deux sont équivalentes.
Toutefois, si on vous demande ed tracer une tangente, c'est la définition la plus pratique.
De même dans les exercice, ce sera la perpendiculaire qui vous sera utile |
| |
Exemple :
|
La distance du centre O du cercle C à la tangente (d) est égale au rayon r du cercle C.
| on dit aussi que : |
- La droite (d) est tangente en H au cercle C;
|
- Le cercle C est tangent en H à la droite (d).
|
|
|
| |
Propriété :
- Un cercle C et la tangente (d) en un point H de ce cercle ont un seul point
d'intersection : le point H.
- H est appelé le point de contact du cercle C et de la tangente (d)
|
|
| |
|
|
| |
III - Bissectrice d'un angle et équidistance |
|
| |
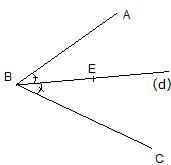
Définition :
La bissectrice d'un angle est la demi-droite qui le coupe en deux angles de même mesure.
|
|
|
| |
Exemple :
|
| |
 |
|
 |
|
 |
|
| On a ABE = EBC, donc la droite (d) est la bissectrice de l'angle ABC |
|
|
| |
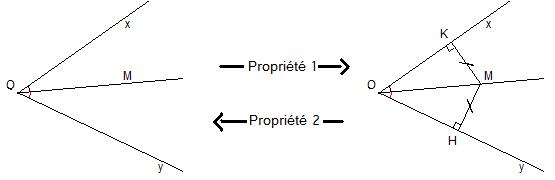
Propriétés :
- Si un point appartient à la bissectrice d'un angle, alors il est équidistant des côtés de cet angle
|
- Si un point situé entre les côtés d'un angle saillant est équidistant des côtés de l'angle, alors il appartient à la bissectrice de cet angle.
|
|
|
C'est cette propriété qui justifie le tracé au compas de la bissectrice d'un angle.
Sinon, ce théorème n'est pas très souvent utiliser, si ce n'est pour justifier l'intersection des trois bissectrices dans un triangle. |
| |
Exemple :
|
M appartient à la bissectrice de
|
|
MH = MK |
| |
 |
|
|
| l'angle xOy |
|
|
| |
IV - Bissectrices d'un triangle et cercle inscrit |
|
| |
Propriété :
Les trois bissectrices d'un triangle sont concourantes en un point appelé le centre du cercle inscrit au triangle
Le cercle inscrit au triangle est tangent aux trois côtés de ce triangle.
|
|
La propriété est à écrire lorsqu'on vous demande de tracer le cercle inscrit d'un triangle,
et ..... c'est tout.... |
| |
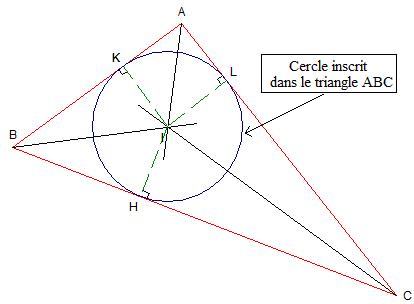
Exemple :
|
| Les bissectrices du triangle ABC sont concourantes en I. |
| I est équidistant des trois côtés du triangle ABC : IH = IK = IL. |
| Le cercle inscrit dans le triangle ABC a pour centre I et pour rayon IH. |
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les distances, tangentes et autres bissectrices |
|
| |
|
Ordre et opérations |
| |
I - Inégalités, valeurs approchées et encadrements |
|
| |
a) Inégalités
|
|
| |
Notations :
- " < " se lit " strictement inférieur à "
|
- " > " se lit " strictement supérieur à "
|
- "
 " se lit " inférieur ou égal à " " se lit " inférieur ou égal à "
|
- "
 " se lit " supérieur ou égal à" " se lit " supérieur ou égal à"
|
|
|
|
| |
Définitions :
a et b désignent deux nombres relatifs :
- "a
 b" signifie que a < b ou que a = b b" signifie que a < b ou que a = b
|
- "a
 b" signifie que a > b ou que a = b b" signifie que a > b ou que a = b
|
|
|
Il faut bien comprendre que cette écriture est moins précise vu qu'on a le choix |
| |
Exemples :
5 = 5 ; donc on peut écrire que 5  5 ou que 5 5 ou que 5  5 5 |
4 > 3 ; donc on peut écrire que 4  3 3 |
-7,5 < -4,3 ; donc on peut écrire que -7,5  -4,3 -4,3 |
|
|
| |
définitions :
- L'inégalité x > 0 signifie que x est strictement positif.
- L'inégalité x < 0 signifie que x est strictement négatif.
- L'inégalité x
 0 signifie que x est positif ou nul. 0 signifie que x est positif ou nul.
- L'inégailité x
 0 signifie que x est négatif ou nul. 0 signifie que x est négatif ou nul.
|
|
|
| |
b) Troncatures et arrondis
|
|
| |
Définitions :
- La troncature à l'unité, au dixième, etc. d'un nombre est obtenue en gardant tous les chiffres du nombre jusqu'au rang indiqué et en supprimant ceux qui suivent.
- L'arrondi à l'unité, au dixième, etc. d'un nombre dépend du chiffre du rang suivant .
|
|
Pour une troncature c'est donc assez simple, on enlève tout ce qui dépasse.
Pour un arrondi, n'oubliez pas de considérer le chiffre suivant..... c'est le seul piège mais qui revient régulièrement le jour du brevet. |
| |
Exemples :
| A la calculatrice on a |
27 |
= 3.28571486, sa troncature au dixième est donc 3,2, |
7 |
| alors que son arrondi au dixième est 3,3 |
- Tous les nombres compris entre 3,2 (inclu) et 3,3 (exclu) ont la même troncature au dixième, égale à 3,2
|
- Tous les nombres compris entre 3,25 (inclu) et 3,35 (exclu) ont le même arrondi au dixième, égale à 3,3
|
|
| |
c) Encadrements
|
|
| |
Définition :
a, b et x désignenet des nombres relatifs.
Lorsque a < x < b ou a  x x  b ou a < x b ou a < x  b ou a b ou a  x < b, on dit que le nombre x est encadré par les nombres a et b. x < b, on dit que le nombre x est encadré par les nombres a et b.
La différence b - a est appelée l'amplitude de cet encadrement.
|
|
Pour placer les crochets, il faut savoir si on prend (ou non) la valeur
limite, ici x < 2 donc 2 n'est pas accepté.
Si on avait eu x  2, alors le crochet aurait été vers l'intérieur. 2, alors le crochet aurait été vers l'intérieur.
|
| |
Exemple :
Si on a 2 < x  5, cela veut dire qu'on peut prendre toutes les valeur comprises entre 2 et 5 sauf 2 5, cela veut dire qu'on peut prendre toutes les valeur comprises entre 2 et 5 sauf 2
par exemple 3,28 |
| on représente cet encadrement ainsi : |
 |
|
| |
II - Comparaison de deux nombres et signe de leur différence |
|
| |
|
Cette définition s'avère très utile à partir de la seconde, où on l'utilise dans l'autre sens,
C'est à dire qu'on commence par dire que la différence est postive (ou négative)
|
| |
Exemples :
|
| |
Propriété :
Pour comparer deux nombres relatifs a et b, il suffit de déterminer le signe de leur différence.
|
|
|
| |
Exemple :
| si x - y = -7, alors x - y < 0 et donc x < y |
|
|
| |
III - ordre et opérations |
|
| |
a) Ordre et addition
|
|
| |
|
pas de problème pour l'additon et la soustraction, c'est la même règle que pour les équations. |
| |
Exemples :
-2 < 5 |
on ajoute 8 |
x - 7  4 |
pour supprimer le -7 et trouver x
on ajoute 7 |
-2 + 8 < 5 + 8 |
x - 7 + 7  4 + 7 |
6 < 13 |
x  11 |
|
|
| |
b) Ordre et multiplication
|
|
| |
Propriété :
a et b désignent deux nombres relatifs et c un nombre strictement positif !!!!!!!!!!! |
- Les nombres a x c et b x c sont rangés dans le même ordre que les nombres a et b
|
|
a |
et |
b |
sont rangés dans le même ordre que les nombres a et b |
| c |
c |
|
|
S'il vous plait, soyez attentif
à ce que vous faites, lorsque vous aurez à résoudre
des inéquations : si vous ne faites pas attention
aux signes lors des multiplications et des divisions vous vous
planterez tout le temps. |
| |
Exemples :
-4 < 3 |
on multiplie par 8
comme 8 > 0, on ne
change pas l'ordre |
-8 |
|
-16 |
on divise par 5
comme 5 > 0, on ne
change pas l'ordre |
-4 x 8 < 3 x 8 |
-8 |
|
-16 |
5 |
5 |
-32 < 24 |
-1,6 |
|
-3,2 |
|
|
| |
Propriété :
a et b désignent deux nombres relatifs et c un nombre strictement négatif !!!!!!!!!!! |
- Les nombres a x c et b x c sont rangés dans l'ordre inverse des nombres a et b
|
|
a |
et |
b |
sont rangés dans l'ordre inverse des nombres a et b |
| c |
c |
|
|
|
| |
Exemples :
3  -2 |
on multiplie par -5
comme -5 < 0, on doit
changer l'ordre |
-16 |
> |
-20 |
on divise par -4
comme -4 < 0, on doit
changer l'ordre |
3 x (-5)  -2 x (-5) |
-16 |
<
|
-20 |
-4 |
-4 |
-15  10 |
4 |
< |
5 |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les inégailtés |
|
| |
|
Géométrie dans l'espace |
| |
I - Pyramides |
|
| |
a) Description et représentation d'une pyramide
|
|
| |
Définition :
Une pyramide est un solide composé :
|
- d'une face polygonale, appelée la base de la pyramide
|
- de faces triangulaires, appelées les faces latérales de la pyramide.
|
Les faces latérales ont un sommet commun, appelé le sommet de la pyramide.
|
|
|
Ces définitions sont assez évidentes, il faut surtout retenir que la hauteur est perpendiculaire à la base, ce qui vous permettra d'employer le théorème de Pythagore |
| |
|
| |
Définition :
La hauteur d'une pyramide de sommet S est le segment [SH], où H est le point
d'intersection de la bese de la pyramide et de la droite perpendiculaire à cette
base passant par le
sommet S.
On appelle aussi hauteur la longueur SH.
|
|
| |
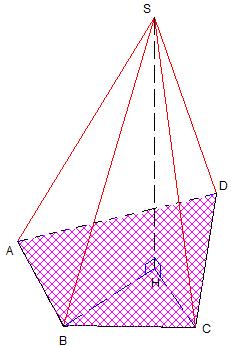
Exemple :
|
Les triangles SAB, SBC, SCD, et SAD sont les faces latérales de la pyramide SABCD.
Le nombre de faces latérales d'une pyramide est égal au nombre de côtés de la base. |
|
|
| |
b) Patrons d'une pyramide
|
|
| |
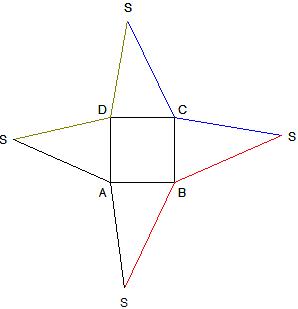
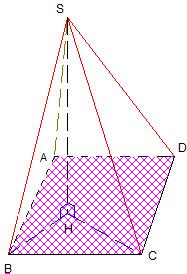
Exemple :
Le patron ci-dessous est un patron de la même pyramide SABCD représenté ci-contre, de base rectangulaire ABCD et de
hauteur [SH].
Les arêtes de la même couleur ont la même longueur |
 |
|
|
Pas de grosses difficultés, il faut bien se rappeler qu'il y a des longueurs qui reviennent plusieurs fois lorsqu'on fait le patron de n'importe quel solide. |
| |
c) Pyramides régulières
|
|
| |
Définition :
Une pyramide est régulière lorsque :
|
- sa base est un polygône régulier, ce qui signifie que ses côtés ont la même longueur et ses angles ont la même mesure.
|
- sa hauteur passe par le centre du cercle circonscrit à la base
|
|
|
Cette définition est importante,
très souvent le jour du brevet on vous dit : "voici une pyramide régulière" et c'est tout,
il faut en déduire que la base est soit un carré, soit un triangle équilatérale,
ce qui aide beaucoup pour les calculs qui suivent.... |
| |
Propriété :
Les faces latérales d'une pyramide régulière sont des triangles isocèles superposables.
|
|
| |
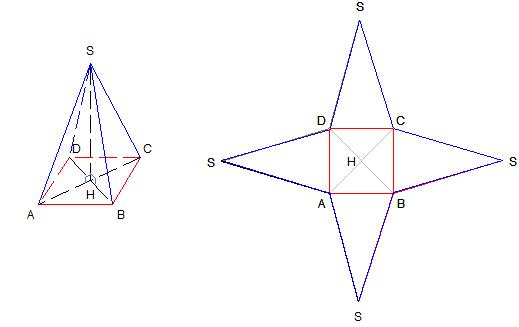
Exemple :
On a représenté ci-dessous une pyramide régulière SABCD et l'un de ses patrons.
Sa base ABCD est un carré de centre H et [SH] est la hauteur de la pyramide. |
|
|
|
| |
II - Cônes de révolution |
|
| |
Définition :
Un cône de révolution est un solide composé :
|
- d'un disque, appelée la base du cône
|
- d'une portion de disque, appelée la surface latérale du cône, dont le centre est le sommet
|
du cône et qui est "enroulée" autour de la base.
|
|
|
Imaginez un cornet de frites ou de glace... |
| |
|
|
| |
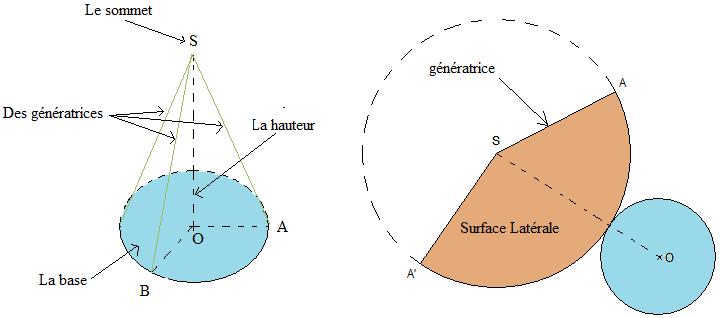
Définition :
- La droite passant par le sommet S d'un cône de révolution et le centre O de sa base est appelée l'axe du cône. Cette droite est perpendiculaire à la base.
|
- La hauteur d'un cône de révolution de sommet S est le segment [SO], où O est le centre de la base. On appelle aussi hauteur la longueur SO.
|
- Tout segment ayant pour extrémités le sommet d'un cône de révotlution et un point du cercle de base est appelé une génératrice du cône.
|
|
|
|
| |
Exemple :
|
Le patron est ce qu'il y a de plus difficile pour le cône, rassurez-vous on ne vous le demandera jamais.
Par contre si vous voulez vérifier,
prenez une feuille et pliez-la pour en faire un cornet, découpez d'abord ce qui dépasse en hauteur, pour en faire un cône et puis coupez le en longueur, vous aurez bien une surface latérale telle qu'elle est déssinez à gauche.... |
| |
III - Volume d'une pyramide et d'un cône de révolution |
|
| |
Propriété :
Le volume d'une pyramide ou d'un cône de révolution est donné par la formule suivante : |
Volume = |
Aire de la base x Hauteur |
= |
1 |
x Aire de la base x Hauteur |
3 |
3 |
|
|
Voila le truc important à retenir de ce chapitre : LA FORMULE :
il n'y a que ça à retenir alors faites un effort, on ne la redonne pas en 3ème et elle sert tous les ans au brevet |
| |
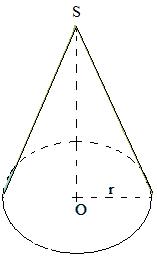
Exemple :
| Calcul du volume du cône de révoltuion ci-contre de hauteur |
|
| SO = 8 cm et dont le rayon de la base est r = 4 cm. |
| |
1) calcul de l'aire de la base :
|
| A = p x r² = p x 4² = 16 p |
| |
| 2) calcul du volume du cône : |
| V = |
1 |
x A x Hauteur = |
1 |
x 16 p x 8 = |
128 |
p |
| 3 |
3 |
3 |
| |
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec la géométrie dans l'espace |
|
| |
|
Proportionnalité et applications |
| |
I - Proportionnalité et représentation graphique |
|
| |
a ) Propriétés
|
|
| |
Propriété :
Si une situation est une situation de proportionnalité,
Alors les points de sa représentation graphique graphique sont alignés avec l'origine du repère
|
|
cette propriété contient donc 2 éléments : l'alignement des points ET le passage par l'origine.
Par habitude, on peut noter x et y dans ce tableau, pour avoir le périmètre d'un carré, on multiplie x par 4 pour avoir y
Ce "y = 4x" est appelé équation de la représentation graphique ce sera très important à partir de la 3ème, alors autant prendre tout de suite cette bonne habitude. |
| |
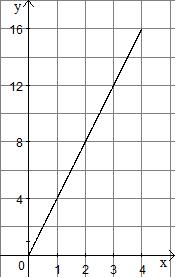
Exemple :
Le périmètre d'un carré est proportionnel à la longueur d'un
de ses côtés, donc les points de la représentation graphique
du périmètre d'un carré en fonction de la longueur d'un de
ses côtés sont alignés avec l'origine du repère. |
 |
Longueur d'un côtés
(en cm) |
0 |
1 |
2 |
3 |
4 |
x |
| Périmètre (en cm) |
0 |
4 |
8 |
12 |
16 |
y = 4x |
|
|
| |
Propriété :
Si les points d'une représentation grahique sont alignés avec l'origine du repère,
Alors ces points représentent une situation de proportionnalité.
|
|
Cette propriété a énormément d'applications, lors d'une expérience, on a automatiquement le graphique par informatique,si celui-ci ressemble à une droite passant par l'origine, on sait qu'il y a un coefficient de proportionnalité.... |
| |
| |
|
| |
b) reconnaissance graphique d'une situation de proportionnalité
|
| |
Les deux propriétés précédentes permettent de savoir si une situation de proportionnalité est ou n'est pas une situation de proportionnalité, en utilisant sa représentation graphique |
| |
Exemples :
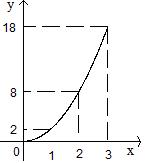
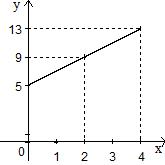
|
|
|
Les points de cette représentation graphique ne sont pas alignés.
Donc cette situation n'est pas de proportionnalité. |
|
Les points de cette représentation graphique ne sont pas alignés avec l'origine du repère.
Donc cette situation n'est pas de proportionnalité. |
|
Les points de la représentation graphique de cette situation sont alignés avec l'origine du repère.
Donc cette situation est de proportionnalité. |
|
|
| |
II - Pourcentages |
|
| |
Un pourcentage traduit une situation de proportionnalité. |
|
| |
Exemples :
Dans une classe de 4ème de 30 élèves, 60 % des élèves pratiquent un sport.
Pour déterminer le nombre d'élèves de cette classe qui pratiquent un sport, on calcul la quatrième proportionnelle du tableau de proportionnalité suivant :
| Nombres total d'élèves |
100 |
30 |
Nombres d'élèves
pratiquent un sport |
60 |
x |
100 x x |
= |
60 x 30 |
x |
= |
60 x 30 |
100 |
x |
= |
18 |
Ainsi 18 èlèves pratiquent un sport dans cette classe |
Dans une classe de 4ème de 30 élèves, 24 élèves sont demi-pensionnaires.
Pour calculer le pourcentage d'élèves demi-pensionnaires dans cette classe, on calcule le nombre de demi-pensionnaires dans une classe de 100 élèves :
| Nombres total d'élèves |
30 |
100 |
Nombres d'élèves
demi-pensionnaires |
24 |
x |
30 x x |
= |
24 x 100 |
x |
= |
24 x 100 |
30 |
x |
= |
80 |
Ainsi 80 % des èlèves sont demi-pensionnaires dans cette classe. |
|
Dans un tableau de proportionnalité on peut utiliser le produit en croix !!!!!!!!!!
Dans ces deux exemples, il est important de faire apparaitre le nombre 100, ce qui s'explique facilement si on lit doucement
pourcentage. |
| |
III - Vitesse moyenne |
|
| |
La vitesse d'un mobile au cours d'un déplacement n'est pas toujours constante.
Ainsi, un TGV a pourcouru 512 km en 2 heures, on peut dire qu'en moyenne il a parcouru 256 km en une heure, ou qu'il a roulé à 256 km/h.
|
|
| |
Définition :
La vitesse moyenne "v" d'un mobile qui a parcouru la distance "d" pendant la durée "t" est donnée par la formule :
|
|
Pas grand chose à dire là-dessus, si ce n'est attention aux pièges des unités. |
| |
Remarques :
L'unité dans laquelle est exprimée une vitesse dépend du choix des untités de distance et de durée.
Par exemple : on peut avoir des km/h (si la distance est en km et la durée en heure) ou des m/s (si la distance est en mètre et la durée en seconde)
On a aussi les formules :
|
|
|
| |
Exemples :
Un train a parcouru 900 km en 3 heures :
sa vitesse est donc v = 900 : 3 = 300 km/h
Un avion a volé pendant 720 secondes à la vitesse moyenne de 270 m/s
la distance qu'il a parcourue d = 270 x 720 = 194 400 m |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec la proportionnalité |
|
| |
|
Statistiques |
| |
I - Vocabulaire |
|
| |
On a pesé douze téléphones portables et obtenu les résultats suivants ( en g)
|
95 ; 105 ; 100 ; 90 ; 95 ; 105 ; 95 ; 105 ; 100 ; 95 ; 100 ; 100 |
- Ces données, c'est à dire ces douzes masses, constituent une série statistique
|
- La population est l'ensemble des téléphones portables
|
- Le caractère étudié est la masse des téléphones portables
|
- Les valeurs de ce caractère sont les différentes masses : 90 ; 95 ; 100 ; 105
|
- L'effectif d'une de ces valeurs est le nombre de fois où celle-ci apparaît , par exemple l'effectif de la valeur 95 est 4
|
|
Pas de commentaire sur ce chapitre qui frise la débilité mentale..... |
| |
II - Moyenne et moyenne pondérée |
|
| |
Définition :
La moyenne d'une série statistique est le quotient de la somme de toutes les données de cette série par son effetif total.
|
|
|
| |
Exemple :
| on souhaite calculer la masse moyenne des téléphones portable : |
| M = |
95 + 105 + 100 + 90 + 95 + 105 + 95 + 105 + 100 + 95 + 100 + 100 |
= |
1 185 |
= 98,75 |
12 |
12 |
| |
|
|
|
|
| Donc la masse moyenne d'un téléphone portable est de 98,75 g |
|
|
| |
Définition :
Pour calculer la moyenne pondérée d'une série statistique, on doit additionner les produits des valeur par leur effectif, puis diviser par l'effectif total.
|
|
|
| |
Exemple :
| on regroupe les données dans le tableau suivant : |
| Masse (en g) |
90 |
95 |
100 |
105 |
| Effectif |
1 |
4 |
4 |
3 |
|
| on souhaite calculer la masse moyenne des téléphones portable : |
| M = |
90 x 1 + 95 x 4 + 100 x 4 + 105 x 3 |
= |
1 185 |
= 98,75 |
12 |
12 |
| |
|
|
|
|
Donc la masse moyenne d'un téléphone portable est de 98,75 g
on retrouve bien le même résultat que précédemment. |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les statistiques |
|
| |
Le programme de 4ème est maintenant terminé, à bientôt pour le programme de troisième ...... |