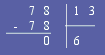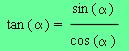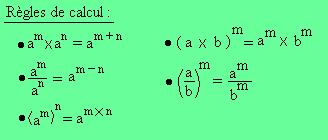|
Le but de ce site est uniquement de vous présenter un cours, et de vous donner des exercices écrits. Si vous cherchez un site d'exercices en ligne, avec corrigés et aide je vous conseille Math En Poche, qui est ce qui se fait de mieux en la matière. Enfin, si jamais vous avez des remarques, n'hésitez pas... |
 |
|
Activité
numérique
|
Activité
géométrique
|
remarque :
Les cours seront toujours construits suivant le même plan : le cours au centre et des commentaires sur les côtés, les commentaires ne sont pas primordiaux, mais ils permettent une meilleure compréhension. Vous trouverez aussi des liens en fin de chapitre vers des exercices du brevet en relation avec le chapitre.
Le cours tient compte du programme précédent l'année 2008, il sera mis à jour le plus vite possible, même si de nombreux chapitres sont identiques.
| I - PGCD de deux nombres entiers positifs | |||||||||||||||||||||||
|
Dans cette partie, les lettres
a et b désignent des nombres entiers positifs
|
|||||||||||||||||||||||
|
Tout ça pour dire
que 3 divise 21 car il existe 7 tel que 21 = 7 x
3
|
||||||||||||||||||||||
|
Exemples :
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
Remarque : Il y a toujours un diviseur commun à deux nombres entiers, car 1 divise tous les nombres. |
|||||||||||||||||||||||
|
Exemples :
|
Pas de panique,ce ne sont
que des exemples, la méthode pour trouver un PGCD vient juste
après ça.
|
||||||||||||||||||||||
|
Première Méthode pour déterminer un PGCD : Lister les diviseurs
remarque : cette méthode ne sera utilisée qu'avec des petit nombres, en effet dès que l'on travaille avec des nombres supérieurs à 50, la recherche des diviseurs est trop laborieuse et on préférera la deuxième méthode : l'algorithme d'Euclide |
Remarque : tous les diviseurs vont par paire. pour 21, on a 1 et 21, puis 3 et 7 Pour 30, on a 1 et 30, puis 2 et 15, puis 3 et 10..... ce qui vous permet de limiter la recherche à la calculatrice. |
||||||||||||||||||||||
|
|||||||||||||||||||||||
|
Exemple : 15 et 26 sont des nombres premiers entre eux, car leur unique diviseur commun est 1. |
|||||||||||||||||||||||
| II - Recherche du PGCD et Algorithme d'Euclide | |||||||||||||||||||||||
|
Ca c'est la théorie,
la démonstration étant complexe en 3ème je
ne la présente pas, la méthode elle vient juste après.
|
||||||||||||||||||||||
|
Exemple :
|
|||||||||||||||||||||||
| intéret : l'avantage de cette propriété est que en continuant le processus de division euclidienne, on va réduire la taille des nombres qui nous interesse | |||||||||||||||||||||||
|
|||||||||||||||||||||||
|
Deuxième méthode pour déterminer un PGCD : l'algorithme d'Euclide.
|
L'avantage de cette méthode est qu'elle est répétitive, donc facile; et quelle ne fait intervenir que des calculs simples : des divisions euclidiennes. Dans la plupart des exercices vous aurez ainsi à poser 3 ou 4 divisions euclidiennes succesives (rarement plus) et le PGCD sera le dernier reste non-nul. |
||||||||||||||||||||||
Utilisation
de la calculatrice :
|
Je sais que la manip n'est
pas simple au premier coup d'oeil, mais entrainez-vous avec les
autres calculs de la page, une fois maitrisée, cette technique
permet de gagner du temps
|
||||||||||||||||||||||
| III - Application du PGCD | |||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
Application : pour rendre un fraction irréductible Ecrire sous forme de fraction irréductible
la fraction Pour cela on utilise le PGCD trouvé dans l'exemple sur l'algorithme d'Euclide. On a PGCD ( 1053 ; 325 ) = 13 donc |
Vous verrez qu'au brevet cette question est toujours en 2 parties a) calculer un PGCD b) simplifier la fraction |
||||||||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec le PGCD
|
|
Ce chapitre est la suite
du chapitre sur le cosinus, vu en 4ème.
|
|
|
Il important de
retenir que tout ce qui va être dit ne concerne que les triangles
rectangles.
|
|
|
De plus, contrairement à
d'autres outils mathématiques, la trigonométrie n'utilise
pas de théorèmes
|
|
|
ce qui simplifie nettement
la rédaction et donc celle-ci se doit d'être parfaite.
|
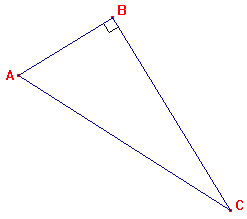
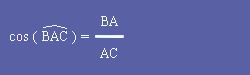
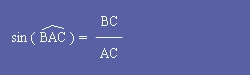
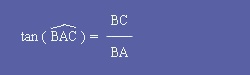
| I - Définition : |
|
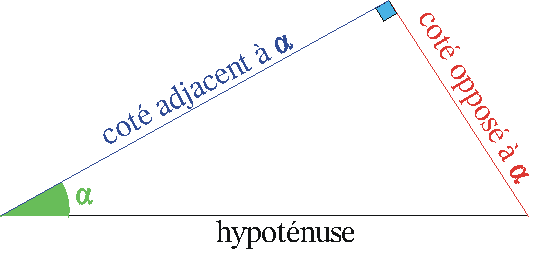 |
|
Ces trois formules sont à connaître par coeur, on va voir au second chapitre leur application. J'insiste, ces formules ne sont valides QUE DANS UN TRIANGLE RECTANGLE. |
||||||||||||||||||||||||||||||||||||
|
C'est l'étape la
plus importante lors de l'utilisation de la trigonométrie.
Il faut être capable de donner le cos, le sin et la tan d'un
angle sans se tromper. Je vous conseille de vous exercer sur mathenpoche
avant de passer aux calculs.
|
||||||||||||||||||||||||||||||||||||
|
Ces formules ne sont pas
très importantes en 3ème, elles le deviennent au lycée.
On les démontre très facilement à l'aide des
définitions.
|
||||||||||||||||||||||||||||||||||||
| II - Applications | |||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
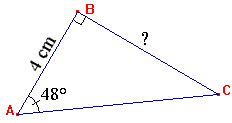
Voici un énoncé typique d'un exercice de brevet. |
||||||||||||||||||||||||||||||||||||
|
Correction :
|
En fait la première étape ici est de déterminer quel outil on va utiliser (cos, sin ou tan) pour cela c'est la figure et la question qui doivent vous aider. Ici on connait le côté adjacent et on cherche le côté opposé...... donc c'est la tangente. |
||||||||||||||||||||||||||||||||||||
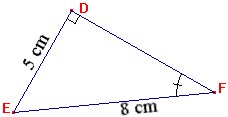
b) pour calculer un angle |
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
Correction :
|
Ici on connait le côté
opposé et
l'hypoténuse, donc
c'est le sinus.
|
|||||||||||||||||||||||||
| Les méthodes : | ||||||||||||||||||||||||||
|
Pour ce chapitre il faut
penser à mettre
 |
|||||||||||||||||||||||||
|
Suivant le modèle de calculatrice, ce n'est pas la même touche, donc à vous de trouver .... Vérifier aussi que vous êtes bien en degrés .... |
|||||||||||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec la trigonométrie
|
| I - Rappel sur les puissances | |||||||||||||||||||||||||||||||||||||||||
|
Dans ce chapitre, m et n
désignent des nombres entiers relatifs, a et b des nombres
relatifs.
|
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
| Remarque : dans le cas où a = 10, on retrouve les règles de calcul sur les puissances de 10. | |||||||||||||||||||||||||||||||||||||||||
| Méthode : pour calculer et mettre en écriture scientifique | |||||||||||||||||||||||||||||||||||||||||
|
Voilà le genre de
question posée régulièrement le jour du brevet.
|
||||||||||||||||||||||||||||||||||||||||
| II - Développer une expression littéral | |||||||||||||||||||||||||||||||||||||||||
|
C'est à dire que
dans le résultat, il ne doit y avoir que des additions et
des soustractions.
|
||||||||||||||||||||||||||||||||||||||||
|
Ces formules ont déjà
été vu en 5ème et en 4ème, souvent illustrées
par des flèches.....
|
||||||||||||||||||||||||||||||||||||||||
Exemple :
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||
| Méthode : pour développer et réduire une expression littérale | |||||||||||||||||||||||||||||||||||||||||
|
Attention à
la règle des signes...
|
||||||||||||||||||||||||||||||||||||||||
| III - Les identités remarquables |
On
va voir 3 formules, les signes seront intégrés dans
ces formules et donc une fois la bonne formule trouvée, plus
besoin de penser aux signes. |
||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
Exemple : développer l'expression
A = ( 2y + 3 )
|
Mettez les parenthèses
au début, ça vous aidera, par la suite vous pourrez
les enlever...
|
||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
attention à la place
du signe -
|
||||||||||||||||||||||||||||||||||||||||
|
Exemple : développer l'expression
A = ( 4y - 5)
|
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
L'ordre des deux parenthèses
n'est pas important, par contre l'ordre de a et b est important..
|
||||||||||||||||||||||||||||||||||||||||
|
Exemple : développer l'expression A = ( 5y - 7 )( 5y + 7 )
|
|||||||||||||||||||||||||||||||||||||||||
| Remarque : ces trois formules
peuvent s'utiliser dans les deux sens, c'est à dire que si
( a + b )( a - b ) = a |
|||||||||||||||||||||||||||||||||||||||||
| on a aussi a |
|||||||||||||||||||||||||||||||||||||||||
| IV - Factoriser une expression | |||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
Donc factoriser, c'est le
contraire de développer.
|
||||||||||||||||||||||||||||||||||||||||
| Exemple : reprenons l'exemple
suivant : ( 2 + y ) ( y + 6 ) = 2y +
12 + y |
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
Ecrit à l'envers,
on retrouve une propriété de 5ème
|
||||||||||||||||||||||||||||||||||||||||
| Exemples : les exemples suivants sont de difficultés croissantes, le dernier est ce qui vous est demandé au brevet. | |||||||||||||||||||||||||||||||||||||||||
|
Dans ce genre d'exercices,
le plus important est de trouver le facteur commun, il est en rouge
pour ces exemples.
|
||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
| exemples : pour factoriser sous la forme .... | |||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
Exemple : factoriser
l'expression suivante : D = ( 3x - 21 )
|
De tout les exemples, c'est
celui-là que les élèves apprécient en
générale le moins. Pourtant la seule difficulté
est de ne pas se tromper dans les signes.
|
||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec le calcul littérale
|
|
I - Le théorème
de Thalès
|
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
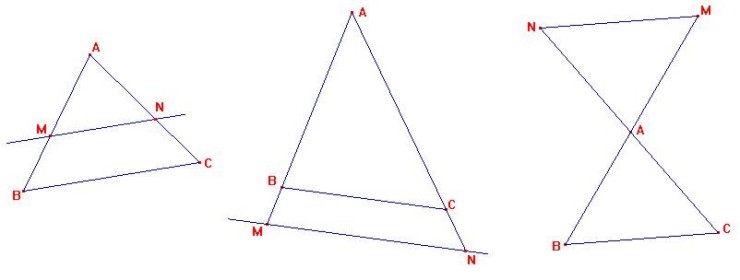
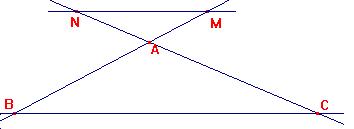
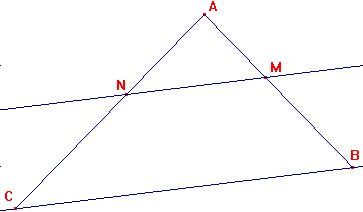
Jusqu'en troisième
le choix d'un théorème lorsqu'on est en exercice est
assez facile, en effet la plupart du temps, la figure "appelle"
le théorème adéquat, on parle de configuration,
voyons les configurations de Thalès :
|
||||||||||||||||||||||||||
|
avec (MN) // (BC) |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
La rédaction de ce
théorème étant très simple, il n'est
toléré aucune erreur dans les données et dans
le nom "Thalès".
|
|||||||||||||||||||||||||
|
méthode
: pour calculer une longueur
|
||||||||||||||||||||||||||
|
Encore une question classique
du brevet...
|
|||||||||||||||||||||||||
|
Rappel : les longueurs
n'ont rien à voir dans les hypothèses, elles permettent
certes de faire les calculs, mais elles ne servent à rien
pour justifier le théorème.
|
|||||||||||||||||||||||||
|
II - La réciproque
du théorème de Thalès
|
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
méthode
: pour démontrer que deux droites sont parallèles
|
||||||||||||||||||||||||||
|
Toujours une question classique
du brevet...
|
|||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec le théorème
de Thalès.
|
| I - Racine carrée d'un nombre POSITIF | |||||||||||||||||
|
Le mot positif est très
important. On verra pourquoi juste après.
|
||||||||||||||||
|
explication
: ca veut dire que le nombre "a"
peut s'obtenir en mettant un autre nombre au carré, et comme
un nombre au carré est toujours positif, voilà pourquoi
"a" doit absolument être positif, sinon on ne peut
pas trouver sa racine carrée.
|
|||||||||||||||||
|
Exemple :
|
Ceci est connu depuis la
quatrième et le cours sur le théorème de Pythagore
|
||||||||||||||||
|
remarque : une racine carrée n'est pas toujours un nombre exact, dans ce cas là on écrit ce nombre grâce à la racine carrée
|
|||||||||||||||||
|
Cette propriété
est très importante pour les exercices.
|
||||||||||||||||
|
|||||||||||||||||
|
Remarque : Si a est un nombre NEGATIF,
alors |
|||||||||||||||||
| Methode : Pour calculer sur des nombres écrits avec racines carrées | |||||||||||||||||
|
Les racines carrées
vont donc se comporter comme des lettres pour le développement
avec des simplifications pour les calculs.
|
||||||||||||||||
| II - Règle de calcul avec les racines carrées | |||||||||||||||||
|
|||||||||||||||||
|
|||||||||||||||||
|
|||||||||||||||||
| Exemples : | |||||||||||||||||
|
|
|||||||||||||||||
| Méthode : Pour calculer une somme de nombres écrits avec des racines carrées | |||||||||||||||||
|
Dans ce genre d'exercice,
le jour du brevet le b est toujours donné : soit dans l'énoncé,
soit dans l'expression (avec un nombre que l'on ne peut décomposer)
|
||||||||||||||||
|
|||||||||||||||||
|
|||||||||||||||||
| Exemple : |
|||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec les racines carrées.
|
|
Remarque :
ce cours changera à la rentrée 2008
|
|||||||||||||||||
| Rappel | |||||||||||||||||
|
|||||||||||||||||
|
|||||||||||||||||
| I - Translation et vecteur | |||||||||||||||||
|
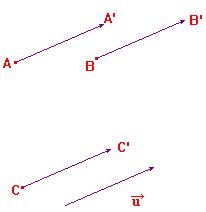
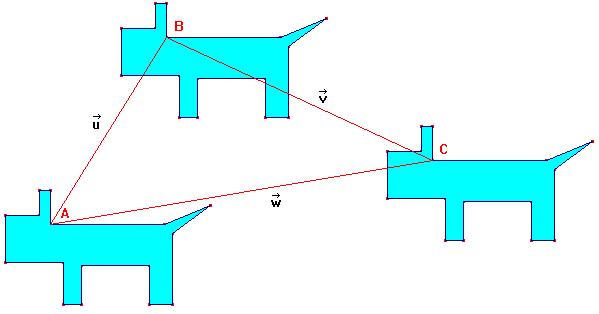
En considérant un
vecteur comme étant le représentant d'un glissement,
la notion de direction, de sens et de longueur paraissent naturelles
et suffisent à définir ce glissement.
|
||||||||||||||||
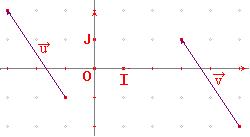
| Exemple :
pour le vecteur |
Si les notions de sens et
de longueur paraissent évidentes, celle de direction peut
paraitre plus compliquée, pour la comprendre il suffit de
considérer que le vecteur donne une "direction"
à suivre sur une carte....
|
||||||||||||||||
- la direction du
vecteur  |
|||||||||||||||||
| - le sens du vecteur |
|||||||||||||||||
| - la longueur du vecteur |
|||||||||||||||||
| - on a |
|||||||||||||||||
| II - égalité de deux vecteurs | |||||||||||||||||
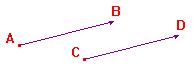
|
Pour démontrer ce
résultat, il suffit de considérer les parallélogrammes
vus avec les translations...
|
||||||||||||||||
|
Les deux premières propriétés sont extrémement utilisées le jour du brevet, elles font intervenir le lien entre vecteur, translation et parallèlogramme. De plus le rédaction se limite à ce qui est écrit ici. |
||||||||||||||||
| III - composée de deux translations et somme vectorielle | |||||||||||||||||
| Remarque : une composée de translations, c'est simplement faire deux translations succéssivement... | |||||||||||||||||
|
La première partie
sert à tracer des constructions, la deuxième sert
à faire des calculs avec des vecteurs (surtout à partir
de la seconde)
|
||||||||||||||||
| Méthode : Pour construire un représentant de la somme de deux vecteurs | |||||||||||||||||
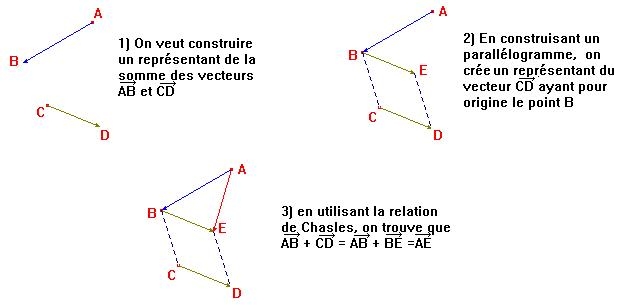 |
Ici on travaille sans quadrillage,
avec un quadrillage il suffit de compter les carreaux...
|
||||||||||||||||
| IV - Composée de deux symétrie centrales | |||||||||||||||||
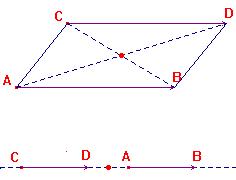
|
La démonstration se fait très facilement avec les théorèmes des milieux Cette propriété s'utilise telle quelle, c'est juste du cours à connaître par coeur. |
||||||||||||||||
|
Exemple :
|
|||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec les vecteurs.
|
|
La leçon sur les équations posent de nombreux problèmes à de nombreux élèves, pour éviter le plus de problèmes, la méthode que j'essaie de faire aplliquer à mes élèves est la suivante :
Ces règles resteront les mêmes pour les inéquations et les équations produit nul. |
|||||||||||||||||||||||||
| I - Résoudre une équation à une inconnue | |||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
Exemple :
|
Pensez que le terme que
l'on déplace arrive toujours après tout le reste....
|
||||||||||||||||||||||||
| II - Résoudre un problème | |||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
Exemple :
|
L'exemple choisi est volontairement
simple, ceci permet de bien assimiler la méthode, à
vous maintenant de l'appliquer en exercices. Cette méthode
fonctionne jusqu'après le BAC, donc autant insister tout
de suite sur son importance...
|
||||||||||||||||||||||||
| III - Equations produit nul | |||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
Méthode
: Pour résoudre un équation une équation
produit nul
|
|||||||||||||||||||||||||
|
Une fois la méthode
comprise, les résolutions sont généralement
très simples.
|
||||||||||||||||||||||||
| IV - équation
x |
|||||||||||||||||||||||||
| A
partir de ce paragraphe, on parlera de nombre strictement positif
(x > 0) ou de nombre positif (x |
|
||||||||||||||||||||||||
|
Les explications ont déjà
été données dans le cours sur les racines carrées,
il suffit de connaitre ce résulat par coeur.
|
||||||||||||||||||||||||
| Rappel : Si a est un nombre strictement négatif, la racine carrée de a n'existe pas donc l'équation n'a pas de solution | |||||||||||||||||||||||||
|
Exemple :
|
|||||||||||||||||||||||||
| V - inégalités et opérations | |||||||||||||||||||||||||
|
Rappel :
|
|||||||||||||||||||||||||
|
S'il vous plait, soyez attentif
à ce que vous faites, lorsque vous aurez à résoudre
des inéquations : si vous ne faites pas attention
aux signes lors des multiplications et des divisions vous vous
planterez tout le temps.
|
||||||||||||||||||||||||
| Méthode : pour résoudre une inéquation | |||||||||||||||||||||||||
|
Résoudre une inéquation
se fait donc de la même manière que résoudre
une équation, mais avec la contrainte supplémentaire
de faire attention aux signes lors des multiplications et divisions.
|
||||||||||||||||||||||||
| Pour savoir comment
faire ce dessin, il suffit de placer le 0 et la valeur trouvée,
puis de tracer dans le bon sens. Pour placer les crochets, il faut savoir si on prend (ou non) la valeur limite, ici x > 2 donc 2 n'est pas accepté. Si on avait eu x |
|||||||||||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec les inéquations.
|
| I - Angle inscrit et angle au centre | |||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
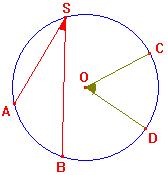
Exemple :
|
Cet exemple
est juste là pour illustrer
la propriété, la rédaction demandée
au brevet est donnée dans l'exemple suivant ...
|
||||||||||||||||||||||||||||
|
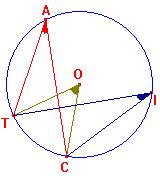
Methode
: Pour déterminer un angle
|
|||||||||||||||||||||||||||||
|
Cet exercice fait partie
des classiques du brevet, pourtant peu d'élèves arrivent
à le réaliser pour la simple raison qu'isl ne "voient"
pas le lien entre le dessin et la propriété, donc
concentrez-vous sur la figure ...
|
||||||||||||||||||||||||||||
| II - Rotation | |||||||||||||||||||||||||||||
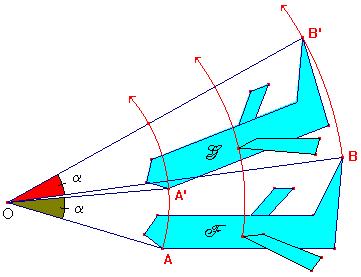
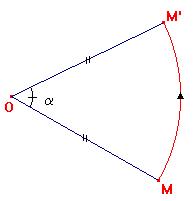
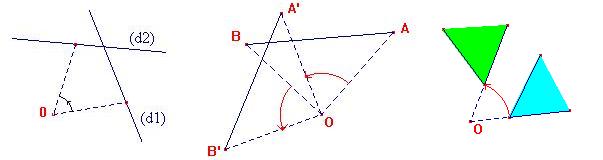
|
Autant vous habituer tout de suite au sens dit trigonométrique, car il devient la norme dès le lycée ... | ||||||||||||||||||||||||||||
| Exemple : | |||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
La plupart des exercices
de brevet sur les rotations sont des exercices de tracé à
l'aide de quadrillage, ces propriétés sont nettement
plus utilisées à partir du lycée ....
|
||||||||||||||||||||||||||||
| III - polygônes réguliers | |||||||||||||||||||||||||||||
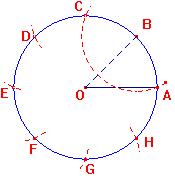
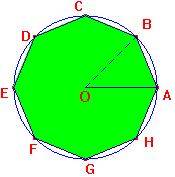
|
|||||||||||||||||||||||||||||
| Exemples : | |||||||||||||||||||||||||||||
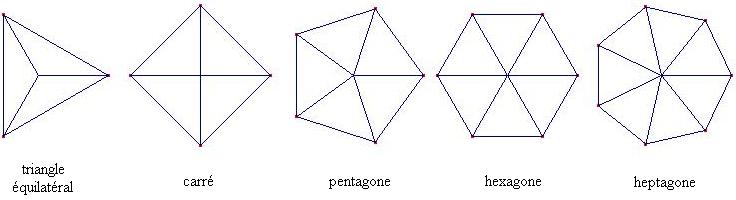 |
|||||||||||||||||||||||||||||
|
Au brevet il est régulièrement
demandé de tracé un polygone régulier, la seconde
propriété permet de justifier cette construction.
|
||||||||||||||||||||||||||||
| Méthode : pour construire un régulier | |||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec les angles.
|
| Ce chapitre provoque chaque année des cauchemards chez une bonne partie des élèves, malheureusement ces difficultés ne viennent que d'un seul facteur : ils considèrent qu'en math il n'y a pas de cours à apprendre : c'est faux et ce chapitre en est la preuve, il n'a rien de compliqué si on apprend le vocabulaire, donc ..... | ||||||||||||||||
| I - fonctions linéaires | ||||||||||||||||
| Préambule
: Lorsque l'on demande à un élève de tracer
l'image d'un point par une symétrie axiale, dès la classe
de sixième, il sait quoi faire. En troisième, on élargit
cette notion de transformation en l'appliquant à des nombres,
on ne parlera alors plus de transformation mais de fonction. La plupart des élèves ont déjà travaillé avec des fonctions mais sans le savoir : les exercices qui commencent par prenez un nombre, ajouter lui 2, puis multipliez le résultat par 3 sont en fait des exercices sur les fonctions : dans cette exemple, la fonction est : ajoutez 2 et multipliez par 3, on verra comment écrire cette fonction dans la suite du cours. |
||||||||||||||||
|
ces trois définitions, forment l'essentiel du cours, le reste n'est qu'une application. les exercices seront de trois
types : dans ces trois cas, il suffira
d'écrire que |
|||||||||||||||
| Donc une fonction linéaire
de coefficient a, c'est juste : prenez un nombre (noté x) et
multipliez le par a, on obtient ax. Ce qu'il faut retenir, c'est que si vous connaissez a, vous connaissez la fonction linéaire. |
||||||||||||||||
|
||||||||||||||||
| Exemple : La fonction linéaire
f de coefficient 2 se note f : x |
||||||||||||||||
|
||||||||||||||||
| Tous les termes de la dernière définition sont importants, il faut absolument comprendre que la fonction f transforme le nombre en un autre nombre, donc f (x) est un nombre, c'est le résultat de la transformation de x par la fonction f. | ||||||||||||||||
| Méthode : pour déterminer l'image d'un nombre par une fonction donnée | ||||||||||||||||
|
La phase 1) est la plus
importante, c'est le point de départ de tout exercice sur
les fonctions
|
|||||||||||||||
| Méthode : pour déterminer un nombre a partir de son image par une fonction | ||||||||||||||||
|
Pour cette exercice il faut
faire attention à la formulation, pour ne pas confondre avec
le 1er exercice.
|
|||||||||||||||
| Méthode : pour déterminer une fonction linéaire à partir de l'image d'un nombre | ||||||||||||||||
|
Déterminer un fonction
linéaire, c'est juste trouver son coefficient a.
|
|||||||||||||||
| II - Application | ||||||||||||||||
|
||||||||||||||||
|
||||||||||||||||
|
Exemple :
|
||||||||||||||||
|
||||||||||||||||
|
||||||||||||||||
| Exemple : | ||||||||||||||||
| Pour prendre 15% de 340, on cherche
l'image de 340 par la fonction linéaire f : x c'est à dire : f (340) = |
Cet exercice et ceux qui
suivent sont totalement inutiles, mais ils sont demandés
au brevet donc...
|
|||||||||||||||
|
||||||||||||||||
| Exemple : | ||||||||||||||||
| Pour effectuer une diminution
de 20 % sur 340, on cherche l'image de 340 par la fonction linéaire
g : x g (340) = |
||||||||||||||||
|
||||||||||||||||
| III - Représentation graphique d'une fonction linéaire | ||||||||||||||||
|
||||||||||||||||
|
||||||||||||||||
|
Chaque partie est importante,
en effet :
|
||||||||||||||||
| Méthode : pour représenter graphiquement une fonction linéaire | ||||||||||||||||
|
Le but de ce genre d'exercice
va être de tracer plusieurs fonctions sur un même graphique
pour pouvoir les comparer, il est donc important de bien noter l'équation
de la fonction comme il est fait sur le dessin.
Il est parfois plus pratique de prendre un point A qui n'a pas pour abcsisse 1. |
|||||||||||||||
|
||||||||||||||||
|
Il est essentiel de comprendre
que la droite que l'on a tracé représente le lien
qu'il y a entre les nombres de départs x et leur image f(x),
d'ailleurs ont obtient l'un ou l'autre en traçant les pointillés
que vous avez pour le point A.
|
||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec les fonctions linéaires.
|
|
Depuis l'entrée au
collège, on voit que géométrie et numérique
sont étroitement liés dans de nombreux théorèmes,
on va généraliser ce processus dans la géométrie
analytique.
|
||||||||||||||||
| I - Repère du plan et coordonnées d'un vecteur | ||||||||||||||||
|
||||||||||||||||
|
Un vecteur définit une translation (qui est un glissement), les coordonnées d'un vecteur explicite ce glissement : 2 carreaux vers la droite et 1 carreau vers le haut. |
|||||||||||||||
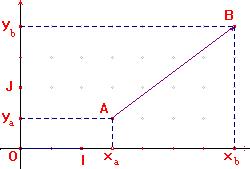
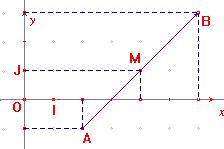
| Exemple : | ||||||||||||||||
| Dans la figure ci-dessus on a : A ( 1,5 ; 0,5 ) et B ( 3,5 ; 2 ) | ||||||||||||||||
| donc : |
||||||||||||||||
|
||||||||||||||||
|
||||||||||||||||
|
Il y aura trois formules
dans ce chapitre, pour répondre aux questions le jour du
brevet, il suffit de connaitre ces formules par coeur ...
|
|||||||||||||||
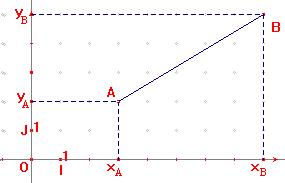
| Exemple : | ||||||||||||||||
| Dans le figure ci-dessus, on a
|
||||||||||||||||
|
||||||||||||||||
|
||||||||||||||||
| II - Longueur dans un plan muni d'un repère orthonormé | ||||||||||||||||
|
||||||||||||||||
| Exemple : | ||||||||||||||||
|
||||||||||||||||
|
Cette formule ne fonctionne
QUE dans un repère orthonormé, alors attention aux
pièges...
|
||||||||||||||||
|
||||||||||||||||
| Methode : pour déterminer une longueur | ||||||||||||||||
|
Renoter la formule est tres
important ici, le jour du brevet, il ya plus de points pour la formule
que pour le résultat .
|
|||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec la géométrie
analytique.
|
|
||||||||||||||||||||||
| I - fonctions affines | ||||||||||||||||||||||
|
Comme dit juste au-dessus,
les principes restent les mêmes, on a juste rajouté
une opération au processus.
|
|||||||||||||||||||||
| Exemple : | ||||||||||||||||||||||
| La fonction affine
f qui à x associe le nombre -3x + 4 se note : f : x |
||||||||||||||||||||||
| l'image de -1 par la fonction f est f (-1) = -3 x (-1) + 4 = 3 + 4 = 7 | ||||||||||||||||||||||
| Remarques : | ||||||||||||||||||||||
| - lorsque b = 0, f (x) = ax, une fonction linéaire de coefficient a | ||||||||||||||||||||||
| - lorsque a = 0, f (x) = b, on dit que f est une fonction constante | ||||||||||||||||||||||
|
Encore une formule à
connaître par coeur...
|
|||||||||||||||||||||
| Méthode : pour déterminer une fonction affine | ||||||||||||||||||||||
|
Il faut bien faire attention à l'ordre dans laquelle on écrit l'égalité, sinon on risque de faire des erreurs de signe... Ensuite le principe reste le même que pour les fonctions linéaires : on utilise les données de l'énoncé |
|||||||||||||||||||||
| II - représentation graphique d'une fonction affine | ||||||||||||||||||||||
|
La représentation
d'une fonction affine est donc une droite QUELCONQUE qui ne passe
pas forcément par l'origine.
|
|||||||||||||||||||||
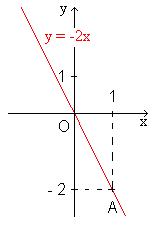
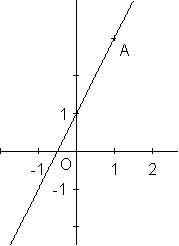
| Exemple : | ||||||||||||||||||||||
| La représentation graphique
de la fonction affine f : x |
||||||||||||||||||||||
| Son coefficient directeur est 2 et son ordonnée à l'origine est 1 | ||||||||||||||||||||||
|
||||||||||||||||||||||
| Méthode : pour tracer une droite d'équation ax + b | ||||||||||||||||||||||
|
La méthode reste
donc la même que pour les fonctions linéaires : on
trace la fonction en définissant des points de passage....
|
|||||||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec les fonction affines.
|
|
La géométrie
dans l'espace au collège a pour but de vous faire découvrir
les problèmes liés à la perspective à
travers l'étude de différentes figures, en classe
de troisième on développe les notions de parallélisme
et d'intersection dans l'espace, toutefois aucun théorème
de géométrie dans l'espace n'est demandé au
brevet, et donc le plus important reste de développer votre
"vision" de l'espace...
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
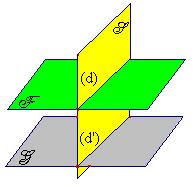
| I - Plan et droite de l'espace | ||||||||||||||||||||||||||||||||||||||||||||||||||||
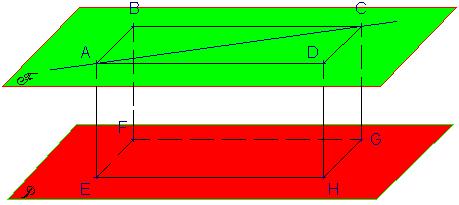
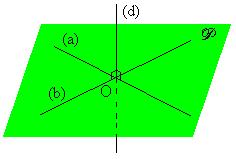
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Exemple : | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Refaire ces figures est
le meilleur entrainement pour acquérir une meilleure vision
de l'espace, pensez dans un premier temps à utiliser les
carreaux
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
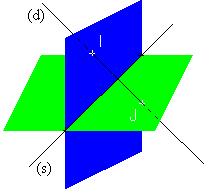
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Exemple : | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
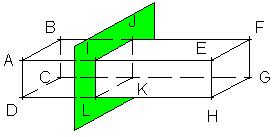
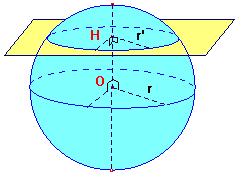
| II - Section par un plan | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Toutes ces propriétés se démontrent facilement avec les définitions données précédemment. Elles sont assez évidentes à retenir, elles servent surtout à justifier des calculs de volume. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
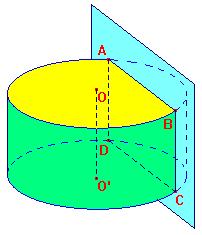
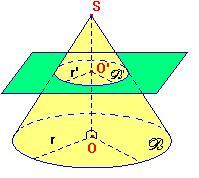
| III - Section d'une pyramide ou d'un cône | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Voila la partie nécessaire le jour
du brevet... |
|||||||||||||||||||||||||||||||||||||||||||||||||||
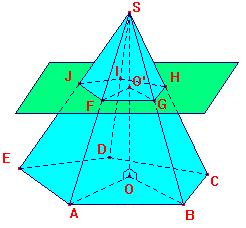
| Exemple : | ||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Voilà le genre de
figures que l'on trouve le jour du brevet souvent "habillé"
de situation réelle, le principe est toutefois toujours le
même, il suffit de connaître ses formules de volume
et d'appliquer le principe suivant, puis de finir les calculs...
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
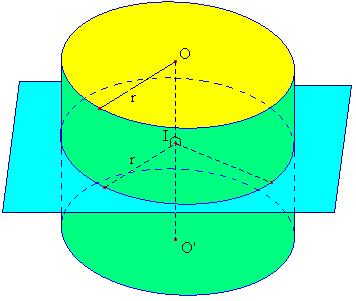
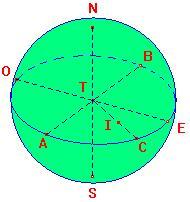
| IV - Sphère et boule | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
C'est à dire que
la sphère est vide et que la boule est pleine...
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
| Exemple : | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Encore deux formules à
connaître par coeur ...
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec la géométrie
dans l'espace.
|
|
Résoudre une équation
sert d'abord à résoudre un problème. Les problèmes
au fil de l'histoire s'étant complexifiés, il a fallu
trouver de nouvelles méthodes pour répondre aux interrogations
(venent souvent de nos amis physiciens....)
Donc après avoir vu les équations du premier degrès à une inconnue, nous allons voir les systèmes de deux équations à deux inconnues. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| I - Systèmes d'équations | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On parle d'un couple de
solutions, car il faut trouver x et y.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Exemple : | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Pour vérifier qu'un
couple est solution, il faut vérifier les deux équations.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Pour résoudre ces
systèmes, on va maintenant voir deux méthodes, elles
fonctionnent toutes les deux, la première va s'appliquer
à des systèmes plus simples, tandis que la seconde
permet d'appréhender ce qui va venir les années suivantes
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Méthode : résolution d'un système d'équation par substitution | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Il est important de numéroter vos équations de départ pour, déjà vous permettre de vous repérer, et surtout pour permettre au correcteur de suivre votre cheminement. Cette méthode ne sera simple que lorsqu'un des coefficients sera égale à 1, donc les autres cas il vous faudra soit maitriser parfaitement le calcul des fractions, soit choisir la seconde méthode... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Méthode : résolution d'un système par l'algorithme de Gauss | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
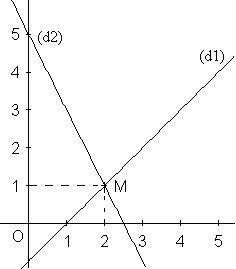
| II - Résolution graphique | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Pour résoudre un
système de deux équations à deux inconnues,
on peut utiliser un graphique.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Exemple : | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce genre de question se
trouve souvent en dernière partie du problème du brevet..
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| III - mise en système d'équation d'un problème | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Exemple : | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce genre d'exercice est
souvent décomposé en deux le jour du brevet, en première
partie, on vous demande de résoudre un système et
ensuite on vous pose un problème dont le système est
exactement le même que le précédent, vous avez
donc déjà les réponses...
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec les systèmes
d'équations..
|
| Ce chapitre est souvent
considérer comme le plus simple de l'année et c'est
le cas.... Il n'y a absolument rien dans ce chapitre, à vous de revoir les calculs de moyenne et de moyenne pondérée. |
|||||||||
| I - Médiane d'une série statistique | |||||||||
|
La médiane sépare
une série en deux si cette série n'est pas ordonnée
(écrite dans l'ordre), la médiane ne veut plus rien
dire, donc ordonnez vos série !
|
||||||||
| Exemple 1 : ( effectif impair ) | |||||||||
| On relève les notes de 9 élèves : 2 ; 6 ; 8 ; 8 ; 11 ; 12 ; 13 ; 15 ; 15 | |||||||||
|
|||||||||
|
|||||||||
| Exemple 2 : ( effectif pair ) | |||||||||
| On note le temps mis par des élèves pour venir au collège : 3 ; 3 ; 5 ; 7 ; 8 ; 8 ; 13 ; 15 | |||||||||
|
|||||||||
|
|||||||||
| Ici, on peut prendre comme médiane de la série un nombre compris entre 7 et 8, par exemple 7,5. | |||||||||
| Remarque : la médiane n'est pas la moyenne, ainsi dans cette exemple la moyenne est de 7,75 (à vous de faire les calculs) | |||||||||
| II - Etendue d'une série statistique | |||||||||
|
|||||||||
| Exemple : | |||||||||
| On considère la série statistique : 8 ; 11 ; 11 ; 13 ; 15 ; 16 ; 16 ; 19 | |||||||||
| L'étendue de cette dérie statistique est 19 - 8 = 11. | |||||||||
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec les statistiques.
|