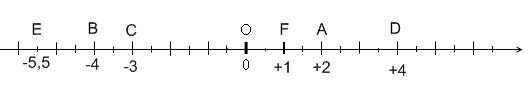|
|
 |
Bonjour, moi c'est profznic, vous
trouverez les cours de cinquième sur cette page.
Le but de ce site
est uniquement de vous présenter un cours, et de vous donner
des exercices écrits.
Si vous cherchez
un site d'exercices en ligne, avec corrigés et aide je vous
conseille Math
En Poche, qui est ce qui se fait de mieux en la matière.
Enfin, si jamais
vous avez des remarques, n'hésitez pas... |
 |
|
| |
| Commençons par le programme : (lien vers les instructions
officielles) |
| |
|
| |
| Et Maintenant les cours
: |
remarque :
- Les cours seront toujours construits
suivant le même plan : le cours au centre et des commentaires
sur les côtés, les commentaires ne sont pas primordiaux,
mais ils permettent une meilleure compréhension. Vous trouverez
aussi des liens en fin de chapitre vers des exercices en relation
avec le chapitre.
|
| |
|
Enchaînements d'opérations |
| |
|
|
| |
Remarque :
-
Dans la plupart des chapitres concernant des règles de calculs, les propriétés sont franchement indigestes, le plus important n'est donc pas de retenir par coeur cette propriété, mais de la comprendre grâce aux exemples qui suivent.
- Tous les calculs doivent être écrits en colonne pour faciliter la lecture des opérations et éviter le plus possible les erreurs. (ce n'est donc vraiment pas pour vous embêter)
 |
- Ce chapitre pose les bases de tout ce qui sera le calcul jusqu'après la terminale, il est donc important de bien assimiler les règles et de faire environ 3 tonnes d'exercices (voir plus ...).
|
|
| |
I - Le signe " = " |
|
| |
Définition :
Le signe " = " associe deux écriture différentes d'un même nombre
|
|
Ca paraît simple, mais les applications sont énormes et bizarrement ça pétrifie les 4ème.... |
| |
Exemple :
| Comme 15 - (5 + 3) = 7 |
et 15 - 2 x 4 = 7 |
| on peut écrire l'égalité : |
15 - (5 + 3) = 15 - 2 x 4 |
|
|
| |
II - Règles de calculs |
|
| |
Théorème :
Si dans un calcul il y a des parenthèses,
Alors il faut d'abord effectuer les opérations entre parenthèses.
|
|
| |
Exemple :
| A = ( 10 + 3 ) x 7 |
| A = 13 x 7 |
| A = 91 |
|
L'écriture en colonne va vous permettre de repérer facilement l'opération à faire et celle restante |
| |
Théorème :
Si dans un calcul il y a plusieurs parenthèses (ou crochets) les unes dans les autres,
Alors il faut d'abord effectuer les calculs dans les parenthèses les plus à l'intérieur.
|
|
|
| |
Exemple :
| B = 5 x [ 12 - (5 - 3)] |
on peut dire que 5 - 3 est un sous-calcul de B, dans ce sous-calcul, il n'y a plus de parenthèses |
| B = 5 x [12 - 2] |
| B = 5 x 10 |
|
| B = 50 |
|
|
|
| |
Théorème :
Si dans un calcul (ou un sous-calcul), il y a plusieurs opérations
Alors il faut effectuer toutes les multiplications et toutes les divisions avant les additions et les soustractions.
|
|
C'est ce qu'on appelle les priorités opératoires, peu importe l'ordre d'écriture, il faut d'abord commencer par les multiplications et les divisions...... |
| |
 |
Commencer par un calcul ne veut pas dire le ré-écrire en premier, vous devez gardez le même ordre pour l'écriture des opérations |
|
..... c'est ici que beaucoup d'élèves se plantent |
| |
Exemples :
| C = 9 - |
20 |
Dans les deux cas, on comence par la multiplication ou la division, mais on écrit le résultat à la place du calcul. |
D = 10 + 3 x 7 |
| 5 |
D = 10 + 21 |
| C = 9 - 4 |
D = 31 |
| C = 5 |
|
|
|
| |
Théorème :
Si, dans un calcul sans parenthèses, il n'y a que des multiplications et des divisions
Alors il faut effectuer les opérations dans le sens de lecture
(de gauche à droite)
|
|
On a vu en 6ème que si il n'y a QUE des multiplications, on peut faire les calculs dans l'ordre qu'on veut, ici ce n'est plus le cas. |
| |
Exemple :
| E = |
7 x 5 |
x 3 |
| |
2 |
| E = |
35 |
x 3 |
| 2 |
| E = 17,5 x 3 |
| E = 52,5 |
|
|
| |
Théorème :
Si, dans un calcul sans parenthèses, il n'y a ques des additions et des soustractions
Alors il faut effectuer les opérations dans le sens de lecture
|
|
On peut faire la même remarque, mais cette fois-ci avec les additions.... |
| |
Exemple :
| F = 7 - 6 + 5 - 3 |
| F = 1 + 5 - 3 |
| F = 6 - 3 |
| F = 3 |
|
|
| |
III - Vocabulaire et convention d'écriture : |
|
| |
a ) Vocabulaire :
|
|
| |
Définition :
| Une expression contenant plusieurs opérations est appelée : |
- une somme si la dernière opération à effectuer est une addition
|
- une différence si la dernière opération à effectuer est une soustraction
|
- un produit si la dernière opération à effectuer est une multiplication
|
- un quotient si la dernière opération à effectuer est une division
|
|
|
ici, le travail consiste à repérer dans quel ordre on devra faire les calculs, le dernier donne le nom de l'expression |
| |
Exemples :
- l'expression 10 + 3 x 7 est une somme
|
|
| car la dernière opération à effectuer est une addition |
| |
- l'expression (2 x 7) x (3 + 5) est un produit
|
| car la dernière opération à effectuer est une multiplication |
|
| |
b ) Convention d'écriture : |
|
| |
Règle :
Lorsqu'une expression contient un quotient, il faut toujours l'imaginer avec des parenthèses autour du numérateur et autour du dénominateur
|
|
Cette règle vous rappelle juste qu'on ne fait pas n'importe quoi avec une fraction |
| |
Exemple :
| 4 + 5 |
peut être pensé comme |
(4 + 5) |
|
| 20 - 8 |
(20 - 8) |
|
|
| |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les priorités opératoires. |
|
| |
| |
|
Construction de triangles |
La géométrie en classe de 5ème à pour but de vous apprendre à justifier toutes vos réponses grâce à des théorèmes du cours, il y a donc plusieurs choses importantes à savoir si on veut réussir sa 5ème :
- Une observation ou des mesures faites sur un dessin ne sont JAMAIS des preuves.
- Des informations sont sûres si elles sont écrites dans l'énoncé ou codées sur le dessin.
- Les théorèmes et définitions sont à connaître par coeur.
|
| |
I - Inégalité triangulaire |
|
| |
Définition :
Trois points non alignés forment un triangle.
|
|
Bizarement quand on demande de placer trois points non alignés, les élèves se trompent ..... |
| |
Exemple :
 |
 |
| Les points forment une droite, ils sont alignés |
Les points ne sont pas alignés, ils forment un triangle |
|
|
| |
Théorème : Inégalité triangulaire
Si une figure est un triangle,
Alors la longueur de chaque côté est plus petite que la somme des deux autres côtés.
|
|
|
| |
Explication : en 6ème on apprend à tracer un triangle au compas, l'inégalité triangulaire vous dit juste que si les traits de compas ne se croisent pas (figure 2), alors on ne peut pas tracer la figure.
 |
 |
ici on a 7 < 3 + 5 (7 < 8)
On peut tracer le triangle |
ici 10 > 3 + 5 (10 > 8)
On ne peut pas tracer le triangle |
|
|
| |
Théorème :
Si trois points A, B et C sont tels que AB + BC = AC
Alors le point A appartient au segment [BC]
|
|
|
| |
Exemple :
 |
AC = AB + BC |
|
|
| |
II - droites remarquables d'un triangle |
|
| |
Avant de commencer cette partie, il vaut mieux revoir les définitions de la médiatrice d'un segment et de la bissectrice d'un angle.
a) Médiatrices :
|
|
| |
Propriété :
Les trois médiatrices d'un triangle se coupent en un même point. On dit qu'elles sont concourantes
|
|
Si cette propriété est facile à voir sur un logiciel, il faut par contre être très précis pour réussir à l'illustrer sur son cahier.... |
| |
Exemple :
 |
ici (d) est la médiatrice du segment [TC],
(d') est la médiatrice du segment [MC]
et (d") est la médiatrice du segment [MT]. |
|
| |
Définition et propriété :
Le cercle circonscrit à un triangle est le cercle qui passe par les trois sommets du triangle.
Le centre du cercle circonscrit à un triangle
est le point d'intersection des trois médiatrices.
|
|
En 5ème on demande aux élèves de savoir tracer le cercle circonscrit, en 4ème on demande aux élèves d'étudier le dernier cas. |
| |
Exemple :
|
| |
b) Bissectrices
|
|
| |
Définition :
Les bissectrices des trois angles d'un triangle se coupent en un même point. Elles sont concourantes
|
|
|
| |
Exemple :
 |
|
 |
|
|
|
| on a : - (d) est la bissectrice de l'angle PVU |
| |
 |
|
|
|
- (d') est la bissectrice de l'angle VPU |
| |
 |
|
|
|
- (d") est la bissectrice de l'angle VUP |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec la contruction de triangles |
|
| |
| |
|
Nombres en écriture fractionnaire |
Rappel :
Lorsqu'on effectue une division, il est rare que la résultat tombe juste, par exemple 1/3 = 0,3333333333333
pourtant, 1/3*3 =1, tandis que 0,333333333333333*3 = 0,999999999999999
On a donc un problème de précision lorsqu'on veut enchainer des calculs
Les fractions sont une solution à ce problème de précision, en effet une fraction n'est composée que de nombres entiers, malheureusement cette précision a un prix, car il faut apprendre à maitriser cette nouvelle écriture.
Une fraction n'est donc que l'écriture précise du résultat d'une division. |
| |
I - Les significations d'une l'écriture fractionnaire |
|
| |
a) Partage |
|
| |
Exemple :
| La surface jaune occupe |
3 |
du rectangle. |
|
| 4 |
| On partage le rectangle en 4 parties égales |
| et on en prend 3 parties sur 4. |
On obtient les |
3 |
du rectangle. |
| 4 |
|
|
| |
b) Quotient de deux nombres
|
|
| |
Définition :
Pour tous les nombres a et b décimaux, avec b différent de zéro,
le quotient du nombre a par le nombre b peut s'écrire
 est le nombre qui multiplié par b donne a est le nombre qui multiplié par b donne a
C'est à dire que :  x b = a x b = a
|
|
|
Pour mémoire, un quotient est juste le résultat d'une division. |
| |
Exemple :
| Le quotient de 7,84 par 2,5 peut s'écrire : |
7,84 |
car : |
| 2,5 |
| |
7,84 |
x 2,5 = 7,84 |
| 2,5 |
|
Cette définition vous dit que si vous divisez une pizza en 4, vous obtenez des quarts de pizza.
puis si vous multipliez 1 quart par 4 vous obtenez votre pizza de départ... autrement dit, diviser par un nombre puis multiplier le résultat par le même nombre vous fait revenir au point de départ.
Pour rappel, 0,33333... n'est pas un nombre décimal car pour être un nombre décimal, il faut qu'à partir d'un moment, les chiffres après la virgule s'arrêtent. |
| |
 |
Une écriture fractionnaire peut être l'écriture de : |
| - un nombre entier : |
42 |
car |
42 |
=6 |
| 7 |
7 |
| - un décimal qui n'est pas un nombre entier : |
4 |
car |
4 |
= 0,8 |
| 5 |
5 |
| - un nombre qui n'est pas un nombre décimal : |
11 |
car ce nombre ne peut pas s'écrire à |
| 3 |
| l'aide d'une fraction décimale |
|
| |
| |
II - multiples et diviseurs |
|
| |
Définition :
Un nombre entier "a" est multiple d'un nombre entier "b" signifie que je peux trouver un nombre "k" pour multiplier "b" et obtenir "a".
Le nombre "b" est alors un diviseur du nombre "a".
|
|
|
| |
Exemple :
| 36 est multiple de 12 car 36 = 12 x 3 |
| 36 est un nombre pair car 2 x 18 = 36 |
| on peut dire aussi que 12 et 2 sont des diviseurs de 36 |
|
| |
III - Egalité de nombres en écriture fractionnaire |
|
| |
Voila la partie la plus merveilleuse des fractions, car on va y apprendre qu'une fraction peut s'écrire d'une infinité de façons.
Bien souvent les élèves sont perturbés par cette propriété, alors qu'en fait c'est super pratique, car dans cette infinité d'écriture, il y en aura forcement une qui va vous arranger........ |
|
| |
Propriété :
Pour obtenir de nouvelles écritures fractionnaires d'un nombre :
Il faut multiplier ou diviser, par un même nombre différent de zéro,
le numérateur et le dénominateur
de ce nombre.
|
|
|
| |
Exemple :
| 1) |
0,5 |
= |
0,5 x 2 |
= |
1 |
2) |
24 |
= |
24 : 6 |
= |
4 |
| 6 |
6 x 2 |
12 |
60 |
60 : 6 |
10 |
|
|
| |
IV - Comparaison de nombres en écriture fractionnaire |
|
| |
Méthode 1 :
si les nombres ont le même dénominateur
Alors ils sont rangés dans le même ordre que leur numérateur.
|
|
|
| |
Exemple :
| 3,5 |
< |
7,2 |
car ces écritures ont le même dénominateur : 8 et 3,5 < 7,2 |
| 8 |
8 |
|
| |
Méthode 2 :
si les nombres ont le même numérateur
Alors ils sont rangés dans l'ordre inverse de leur dénominateur.
|
|
Forcement si on divise un même nombre, celui divisé par le plus grand nombre formera les plus petits morceaux. |
| |
Exemple :
| 15 |
> |
15 |
car ces écritures ont le même numérateur 15 et 13 < 17 |
| 13 |
17 |
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les fractions |
|
| |
|
Symétries centrales |
| |
En 6ème, les élèves étudient la symétrie axiale, c'est à dire par rapport à une droite.
En 5ème l'étude des transformations se poursuit avec la symétrie centrale, c'est à dire par rapport à un point. |
|
| |
I - Définition et vocabulaire |
|
| |
Définition :
On dit que deux figures sont symétriques par rapport à un point si elle se superposent après un demi-tour autour de ce point.
On appelle ce point le centre de symétrie.
|
|
Pour rappel, une symétrie axiale donnait l'impression de voir la figure dans un miroir.
Le principe de ces deux transformations n'est donc pas du tout le même. |
| |
Exemple :
On a fait faire un demi-tour autour du point O à la figure 1) pour obtenir la figure 2)
on peut dire que ces deux figures sont symétriques par rapport à O.
|
| |
Définition :
Dans une symétrie centrale, deux point sont symétriques si le centre de symétrie est le milieu de ces deux points.
|
|
Cette définition est la plus importante car c'est grâce à elle que l'on peut effectuer tous les tracés demandés en 5ème.
Truc important :
pour réussir ses figures toujours tracer les symétriques un point après l'autre et ne jamais chercher à aller trop vite
|
| |
Exemple :
|
| |
Vocabulaire :
on dit que :
- Le dessin A est le symétrique du dessin B par la symétrie centrale de centre S ;
- Le dessin B est l'image du dessin A par cette symétrie centrale ;
- Les dessins A et B sont deux dessins symétriques par rapport à S ;
- Les points M et N sont deux points symétriques par rapport à S.
|
|
|
| |
II - Centre de symétrie d'un dessin |
|
| |
Définition :
Un point est le centre de symétrie d'un dessin si, par symétrie centrale autour de ce point, ce dessin et son symétrique sont confondus.
|
|
C'est à dire que si vous faites tourner la figure autour de ce point, vous obtenez la même figure. |
| |
Exemple :
Les lettres Z et N ont un centre de symétrie, c'est le milieu de la barre oblique .
La lettre T n'a pas de centre de symétrie, mais elle a un axe de symétrie . |
|
|
| |
III - Propriété de la symétrie centrale |
|
| |
Théorème :
La symétrie conserve les longueurs, les angles, l'alignement et les aires.
|
|
L'avantage de ce théorème est qu'on peut le citer en utilisant juste ce qui nous interesse. |
| |
Exemple :
 |
Les triangles DGF et D'G'F' sont symétriques par rapport à S
La symétrie conserve les aires
donc l'aire de ces deux triangles est la même. |
|
Voilà le genre de rédaction que les élèves doivent donner en devoir |
| |
Théorème :
Si deux droites sont symétriques par rapport à un point
Alors elles sont parallèles.
|
|
|
| |
Exemple :
 |
Les droites (d) et (d') sont symétriques par rapport à O
donc elles sont parallèles |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec la symétrie centrale |
|
| |
| |
|
Proportionnalité |
| |
I - Proportionnalité |
|
| |
a) Grandeurs proportionnelles
|
|
| |
Définition :
Dire que deux grandeurs sont proportionnelles signifie que l'on peut calculer l'une à partirde l'autre en multipliant (ou en divisant) toujours par le même nombre.
Ce nombre s'appelle le coefficient de proportionnalité.
|
|
| |
Les élèves peinent à visualiser le principe de proportionnalité, alors imaginer ceci :
Prenez un visage que vous regarder à la loupe grossissement x2, sauf que pas de chance, les oreilles dépassent.
On vous demande alors de faire un dessin correct de ce visage, pour réussir ce dessin, vous serez obligé de multiplier leur taille par 2, car rajouter 4 cm ne suffirait, en effet où rajouter ces 4 cm, sur le haut de l'oreille ou sur le bas......
Alors que si vous multipliez, l'augmentation sera bien répartie.
|
|
| |
Exemples :
1) Pour une petite quantité de baguettes, le prix s'obtient en multipliant toujours le nombre de baguettes par le prix à l'unité.
Le prix est donc proportionnel au nombre de baguettes achetées. |
2 ) Le périmètre d'un carré s'obtient en multipliant toujours la longueur du carré par 4.
Le périmètre d'un carré est donc proportionnel à la longueur du côté. |
Contre-exemple :
| Le nombre de cheveux d'une personne n'est pas proportionnel à son âge. En effet, le nombre de cheveux ne s'obtient pas en multipliant l'âge de cette personne par un nombre. |
|
|
| |
b) Tableau de proportionnalité
|
|
| |
Définition :
Dire qu'un tableau à deux lignes est un tableau de proportionnalité signifie que les valeurs de l'une des lignes s'obtiennent en multipliant toujours par le même nombre les valeurs correspondantes de l'autre ligne.
Ce nombre s'appelle le coefficient de proportionnalité.
|
|
|
| |
Exemple :
| Le tableau ci-dessous est un tableau de proportionnalité : |
| 5 |
7 |
4,5 |
 |
| 2 |
2,8 |
1,8 |
|
| Le coefficient de proportionnalité |
| est donc le quotient de 2 par 5, c'est à dire : |
2 |
| 5 |
| On a |
2 |
= |
2,8 |
= |
1,8 |
|
| 5 |
7 |
4,5 |
|
| |
| Théorème : |
| |
Dans un tableau de proportionnalité composé de deux lignes on peut compléter une colonne : |
| |
- par somme ou différence de deux autres colonnes ;
|
| |
- en multipliant ou en divisant les valeurs d'une autre colonne par un même nombre.
|
|
|
|
| |
Exemple :
| On considère le tableau de proportionnalité précédent et on le complète comme ci-dessous : |
| |
 |
|
 |
|
| 5 |
7 |
12 |
4,5 |
9 |
| 2 |
2,8 |
4,8 |
1,8 |
3,6 |
|
| |
 |
|
 |
|
|
|
|
| |
II - Pourcentage |
|
| |
Définition :
Un pourcentage est un coefficient de proportionnalité de dénominateur 100.
|
|
|
| |
Exemple :
| Faire une remise de 15 % sur tous les prix d'un magasin signifie que pour chaque prix la remise se calcule en |
| multipliant le prix par |
15 |
|
| 100 |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec la proportionnalité |
|
| |
|
Parallélogramme |
| |
Dans ce chapitre, vous verrez de nombreux théorèmes très courts,
le but est donc d'apprendre aux élèves à utiliser les bons outils mathématiques aux bons endroits,
pour cela il faut connaitre ces théorèmes et surtout apprendre à bien lire les énoncés et la question posée. |
|
| |
I - Définition : |
|
| |
Définition :
Si un quadrilatère est un parallélogramme
Alors
ses côtés opposés sont parallèles.
|
|
Ces théorèmes qui se ressemblent beaucoup ne s'utilisent pas de la même façon, tout va dépendre de la
question posée.
le truc c'est que ce qui suit le "Alors"doit répondre à la question. |
| |
Exemple :
 |
ABCD est un parallélogramme. |
|
| |
Théorème :
Si un quadrilatère est un parallèlogramme
Alors ses côtés opposés sont parallèles
|
|
| |
II - Parallélogramme et diagonales |
|
| |
Théorème :
Si un quadrilatère a ses diagonales qui se coupent en leur milieu
Alors ce quadrilatère est un parallélogramme.
|
|
|
| |
Exemple :
| Démontrez que la figure suivante est un parallèlogramme. |
 |
Conditions d'utilisation : |
Conclusion : |
- un quadrilatère
- Les diagonales se coupent en leur milieu |
Ce quadrilatère est un parallélogramme |
|
|
| |
Théorème :
Si un quadrilatère est un parallélogramme
Alors ses diagonales se coupent en leur milieu.
|
|
|
| |
Exemple :
| Démontrez que dans la figure suivante les diagonales se coupent en leur milieu. |
 |
Conditions d'utilisation : |
Conclusion : |
| - un parallélogramme |
les diagonales se coupent en leur milieu |
|
On voit bien ici, que ces deux théorèmes très proches ne répondent pas à la même question. |
| |
Vocabulaire :
On dit que les deux théorèmes précédents sont réciproques, car les conditions d'utilisation de l'un sont la conclusion de l'autre.
|
|
|
| |
Remarque :
On peut démontrer très facilement que le point d'intersection des diagonales d'un parallélogramme est son centre de symétrie.
Cette propriété est peut-être la plus importante, car elle permet de démontrer toutes les autres propriétés du parallélogramme. Mais c'est aussi la plus difficile à utiliser, voila pourquoi, on ne demande jamais aux élèves de l'utiliser.
|
|
| |
III - Parallélogramme et côtés |
|
| |
Théorème :
Si un quadrilatère est un parallélogramme
Alors ses côtés oppposés sont de même longueur.
|
|
|
| |
Exemple :
| Démontrez que dans la figure suivante les côtés opposés ont la même longueur. |
 |
Conditions d'utilisation : |
Conclusion : |
| - un parallélogramme |
les côtés opposés ont la même longueur. |
|
|
| |
Théorème :
Si un quadrilatère a ses côtés oppposés qui ont de même longueur
Alors ce quadrilatère est un parallélogramme.
|
|
|
| |
| Démontrez que dans la figure suivante est un parallélogramme. |
THRD est un quadrilatère tel que : TH = RD = 8 cm
et TR = HD = 2 cm |
Conditions d'utilisation : |
Conclusion : |
- un quadrilatère
- les côtés opposés ont la même longueur |
ce quadrilatère est un parallélogramme |
|
|
| |
IV - Parallélogramme et angles |
|
| |
Théorème :
Si un quadrilatère est un parallélogramme
Alors ses angles opposés ont la même mesure.
|
|
|
| |
Exemple :
| Démontrez que dans la figure suivante les angles opposés ont la même mesure. |
 |
Conditions d'utilisation : |
Conclusion : |
| - un parallélogramme |
les angles opposés ont la même mesure. |
|
|
| |
Théorème :
Si un quadrilatère a ses angles opposés ont la même mesure
Alors ce quadrilatère 'est un parallélogramme.
|
|
|
| |
| Démontrez que dans la figure suivante est un parallélogramme. |
 |
Conditions d'utilisation : |
Conclusion : |
- un quadrilatère
- les angles opposés ont la même mesure |
ce quadrilatère est un parallélogramme |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices du brevet en relation avec les parallélogrammes |
|
| |
|
Les nombres relatifs |
| |
I - Nombres relatifs |
|
| |
Définition :
Un nombre relatif est formé d'un signe + ou - et d'un nombre appelé distance à zéro.
|
|
Vous connaissiez déjà les nombres positifs, pour les négatifs imaginez simplement un hiver très froid et vous aurez des températures en dessous de zéro donc négatives.
La difficulté est qu'il va maintenant falloir apprendre à maîtriser ces nombres et voir tout ce qu'on peut faire avec. |
| |
Exemple :
- (+5) est un nombre relatif :
- son signe est +
- sa distance à zéro est 5
|
- (-3) est un nombre relatif :
- son signe est -
- sa distance à zéro est 3
|
- 0 ; +2 ; + 7,65 ; +
 ; ;
sont des nombres relatifs positifs
|
- 0 ; -3 ; -6,3 ; -

sont des nombres relatifs négatifs
|
|
| |
II - Repérage |
|
| |
a) Sur une droite graduée
|
|
| |
Définition :
Sur une droite graduée, chaque point est repéré par un nombre relatif.
On dit que ce nombre est l'abscisse de ce point.
|
|
|
| |
Exemple :
|
L'abscisse de A est (+2). on note A (+2)
La distance à zéro de (+2) est la distance
du point A à l'origine O du repère.
De même on note :
B (-4) ; C (-3) ; D (+4) ; E (-5,5) et F (+1) |
|
|
| |
b) Dans un repère du plan
|
|
| |
Définition :
Un repère du plan est composé de deux droites graduées de même origine.
L'une est appelée axe des abscisses et l'autre axe des ordonnées.
Un repère du plan est dit orthogonal si ces deux droites sont perpendiculaires.
|
|
|
| |
Exemple :
Dans un repère du plan, la position d'un point est donnée par un couple de nombres relatifs appelé les coordonnées du point.
Le premier nombre est appelé l'abscisse du point.
Le second nombre est appelé l'ordonnée du point.
 |
A a pour coordonnées (+3 ; +1) et on note A (+3 ; +1)
(+3) est l'abscisse de A
(+1) est l'ordonnée de A.
De même on a G (0 ; +4) et C (-1 ; +2) |
|
|
| |
III - Comparaison |
|
| |
Propriété :
- De deux nombres positifs, le plus grand est celui qui a la plus grande distance à zéro.
- De nombres de signes contraires, le plus grand est le nombre positif.
- De deux nombres négatifs, le plus grand est celui qui a la plus petite distance à zéro.
|
|
On visualise très bien cette propriété sur une droite graduée, le plus grand nombre est toujours celui le plus à droite. |
| |
Exemple :
|
- (-5) et (-3) sont négatifs. 3 est plus petit que 5
donc (-3) > (-5)
- (-12) et (+2) sont de signes contraires. (+2) est positif
donc (+2) > (-12)
- (+2) et (+4) sont positifs. 4 est plus grand que 2
donc (+4) > (+2)
|
|
| |
IV - Opérations sur les nombres relatifs |
Pour réussir ces calculs vous devez ABSOLUMENT vous donner une image de ce qui se passe :celle qui fonctionne le mieux est pour moi celle de l'ascenseur :
Si vous montez deux fois vous serez forcement au-dessus du sol (et donc positif)
Si vous descendez deux fois, vous serez forcement en-dessous du sol (et donc négatif)
Si vous montez puis descendez, tout va dépendre de combien,
si vous êtes plus monté, le résultat sera positif et si vous êtes plus descendu, il sera négatif
et on saura où vous êtes en faisant la différence des étages montés et descendus |
| |
a) Somme de deux nombres relatifs
|
| |
Théorème :
Si deux nombres relatifs sont de même signe
Alors
leur somme a aussi le même signe et a pour distance à zéro la somme des distances à zéro des deux nombres.
|
|
| |
Exemple :
|
| |
Théorème :
Si deux nombres relatifs sont signes contraires
Alors
leur somme a le signe du nombre qui a la plus distance à zéro
et a pour distance à zéro la différence des deux distances à zéro.
|
|
| |
Exemple :
(-2) + ( +5) = ?????
- 5 > 2, donc la somme de (+5) et (-2) sera positive : +
- 5 - 2 = 3
(-2) + ( +5) = (+3) |
(+3) + (-8) = ???????
- 8 > 3, dons la somme de (-8) et (+3) sera négative : -
- 8 - 3 = 5
(+3) + (-8) = (-5) |
|
| |
Définition :
Dire que deux nombres sont opposés signifie que leur somme est égale à zéro.
|
|
|
| |
Exemple :
| (-12) + (+12) = 0, donc (+12) et (-12) sont opposés |
|
|
| |
b) Différence de deux nombres relatifs
|
Il faut énormément s'entraîner sur ces calculs pour bien les maitriser, la partie qui va suivre permet d'effectuer des calculs plus longs, mais si vous ne maitrisez pas les calculs simples, alors ça ne sert à rien d'aller plus loin |
| |
Théorème :
Soustraire un nombre, c'est ajouter son opposé.
|
|
| |
Exemple :
(+4) - (-7) = ??????
- le nombre à soustraire est (-7)
- (+7) est l'opposé de (-7)
- soustraire (-7) revient à additionner (+7)
(+4) - (+7) = (+4) + (+7) = (+11) |
|
| |
V - Convention d'écritures |
| |
Règle :
Dans une suite d'additions de nombres relatifs, on peut :
- supprimer les signes d'additon et les parenthèses autour des nombres ;
- supprimer le signe "+" devant un nombre s'il se trouve en début de ligne .
|
|
| |
Exemple :
| A = (+6) + (-7) + (-3,5) + (+9,2) |
|
| A = (+6) + (-7) + (-3,5) + (+9,2) |
On supprime les signes d'addition et les parenthèses autour des nombres |
| A = +6 - 7 - 3,5 + 9,2 |
On supprime le signe "+" en début de ligne |
| A = 6 - 7 - 3,5 + 9,2 |
on regroupe les nombres positifs en début de ligne |
| A = 6 + 9,2 - 7 - 3,5 |
on additionne les nombres positifs ensemble et les nombres négatifs ensemble. |
| A = 15,2 - 10,5 |
on finit par la soustraction. |
| A = 4,7 |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les nombres relatifs |
|
| |
|
Les droites remarquables du triangle |
| |
On a vu dans le chapitre sur les triangles que les médiatrices et les bissectrices d'un triangle sont des droites remarquables, car elles se coupent en un même point.
On va voir maintenant qu'il y a deux autres droites remarquables dans le triangle.
Les définitions sont à savoir absolument par coeur, car de nombreux exercices de 4ème utilisent ces droites remarquables. |
|
| |
I - Hauteur d'un triangle |
|
| |
Définition :
Une hauteur d'un triangle est une droite qui est perpendiculaire à un côté et qui passe par le sommet opposé à ce côté.
On dit aussi qu'une hauteur est relative à un côté ou qu'une hauteur est issue d'un sommet.
|
|
|
| |
Exemple :
 |
(AH)  (BC) et A (BC) et A  (AH) (AH)
on dit que :
- la hauteur (AH) est relative au côté [BC] ;
- la hauteur (AH) est issue du sommet A. |
 |
La hauteur (AH) peut être extérieure au triangle. |
|
|
| |
 |
En fonction de l'exercice, l'expression " hauteur d'un triangle" peut désigner une droite, un segment ou une longueur. |
|
|
| |
II - Médiane d'un triangle |
|
| |
Définition :
Une médiane d'un triangle est une droite qui passe par un sommet et qui passe par le milieu du côté opposé à ce sommet .
On dit aussi qu'une médiane est issue d'un sommet ou qu'une médiane est relative à un côté.
|
|
|
| |
Exemple :
 |
(AM) est la médiane issu ede A dans le triangle ABC |
|
|
| |
 |
- Une médiane est toujours à l'intérieur du triangle.
- En fonction de l'exercice, l'expression " médiane d'un triangle" peut désigner une droite, un segment ou une longueur.
|
|
|
| |
III - triangles particuliers |
Voilà les théorèmes que vous devrez utiliser en 4ème....... à connaître aussi par coeur.....
Ces théorèmes permettent de passer d'une droite remarquable à l'autre et donc d'ajouter des propriétés : d'une hauteur perpendiculaire je peux passer au milieu grâce à la médiane, ce qui est très pratique, je peux choisir ce qui m'arrange en fonction de la question. |
| |
Théorème :
Si un triangle est isocèle
Alors la médiane, la hauteur, la bissectrice issue du sommet principale et la médiatrice de la base sont des droites confondues.
|
|
| |
Exemple : Démontrer que D est le milieu de [JB]
 |
- (DP) est la hauteur issue de P du triangle JPB isocèle en P
- Si un triangle est isocèle
Alors la médiane, la hauteur issue du sommet principale sont des droites confondues
- donc (DP) est la médiane issue de P du triangle JPB et D milieu de [JB]
|
|
| |
Théorème :
Si un triangle est équilatéral
Alors la médiane, la hauteur, la bissectrice issue d'un même sommet et la médiatrice du côtés opposé à ce sommet sont des droites confondues.
|
|
| |
| Exemple : Soit ABC un triangle équilatéral |
| Démontrer que (AH) coupe l'angle |
 |
en deux parties égales. |
| BAC |
 |
- (AH) est à la médiatrice du côté [BC] du triangle ABC équilatéral
|
- Si un triangle est équilatéral
Alors la la bissectrice issue d'un sommet et la médiatrice du côtés opposé à ce sommet sont des droites confondues.
|
- Donc (AH) est la bissectrice de l'angle
|
 |
, elle |
| BAC |
| coupe cet angle en deux parties égales. |
|
|
|
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les droites ramarquables du triangle |
|
| |
|
Expressions littérales |
| |
I - Vocabulaire et convention : |
|
| |
Une expression littérale est une expression contenant des lettres. Elle peut servir à écrire une formule ou encore traduire l'énoncé d'un problème. |
|
| |
Convention :
On peut supprimer le signe x entre deux lettres, entre un nombre et une lettre ou encore devant une parenthèse.
|
|
|
| |
Exemple :
- "a x b" peut s'écrire "ab"
|
- "3 x x" peut s'écrire "3x"
|
- "5 x (2 + x)" peut s'écrire "5(2 + x)"
|
- "c x (x + 4)" peut s'écrire "c(x + 4)"
|
|
| |
Propriétés :
- Multiplier un nombre par 1 ne change pas la valeur de ce nombre :
"1 x x" peut s'écrire "x"
- On peut changer l'ordre des facteurs dans un produit sans en changer le résultat, donc :
"ba" peut s'écrire "ab"
- Multiplier un nombre par 0 donne toujours le résultats 0 :
"0 x x" peut s'écrire 0
|
|
| |
II - Développer et factorisr une expression littérale |
|
| |
Propriété :
Pour tous les nombres k, a et b, on a les formules suivantes :
- k x (a + b) = k x a + k x b
|
- k x (a - b) = k x a - k x b
|
|
|
Ca peut paraître compliqué, mais ce ne sont vraiment que deux formules à appliquer, beaucoup d'exercices devraient vous rassurer |
| |
Remarque :
- Une égalité est vraie dans les deux sens, on a donc aussi les formules suivantes :
|
| k x a + k x b = k x (a + b) |
et k x a - k x b = k x (a - b) |
|
|
| |
Vocabulaire :
Factoriser une somme ou une différence, c'est donner une autre écriture de cette somme ou cette différence sous la forme d'un produit plus utile pour résoudre un problème.
Pour factoriser en 5ème, on utilise les égaliltés suivantes :
| k x a + k x b = k x (a + b) |
et k x a - k x b = k x (a - b) |
|
|
|
| |
Exemple 1 : calculer de tête 7 x 125 + 7 x 75
| 7 x 125 + 7 x 75 |
on commence par repérer le facteur commun |
| puis on factorise grâce à la formule : |
| 7 (125 + 75) |
|
| 7 x 200 |
il n' y a plus qu'à finir les calculs en utilisant les priorités opératoires |
| 1400 |
|
Le changement d'écriture a permis de beaucoup simplifier les calculs. |
|
| |
Exemple 2 :
| Factoriser l'expression suivante : 5 x x - 5 x 7 |
| |
5 ( x - 7) |
|
|
| |
Vocabulaire :
Développer un produit, c'est donner une autre écriture de ce produit sous la forme d'une somme ou d'une différence plus utile pour résoudre un problème.
Pour développer en 5ème, on utilise les égaliltés suivantes :
| k x (a + b) = k x a + k x b |
et k x (a - b) = k x a - k x b |
|
|
| |
Exemple 1 : calculer de tête 12 x 103
| 12 x 103 |
on écrit ce calcul de sorte à faire apparaître un produit développable : |
| 12 (100 + 3) |
On développe grâce à la formule : |
| 12 x 100 + 12 x 3 |
|
| 1200 + 36 |
il n' y a plus qu'à finir les calculs en utilisant les priorités opératoires |
| 1236 |
|
Le changement d'écriture a permis de beaucoup simplifier les calculs. |
|
| |
Exemple 2 :
| Développer l'expression suivante : 3 (8 - x) |
| |
3 x 8 - 3 x x |
| |
24 - 3x |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les expressions littérales |
|
| |
|
Angles et parallélisme |
| |
I - Vocabulaire |
|
| |
Définition :
- Dire que deux angles sont complémentaires signifie due leur somme est égale à 90°.
- Dire que deux angles sont supplémentaires signifie que leur somme est égale à 180°.
|
|
Pour ne pas mélanger ces définitions, il faut utiliser le premier son des mots :
QUE pour complémentaire et QUE pour 90
SE pour supplémentaire et SE pour 180 |
| |
Exemple :
|
| |
Définition :
Dire que deux angles sont adjacents signifie que :
- Ils ont le même sommet ;
- Ils ont un côté en commun ;
- Ils sont de part et d'autre de ce côté commun.
|
|
En gros deux angles adjacents sont des angles collés l'un à l'autre.... mais attention aux pièges |
| |
Exemple :
 |
 |
| |
 |
|
 |
|
 |
|
 |
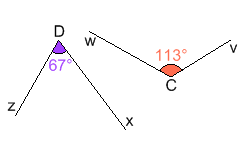
| Les angles uBv et vBt sont adjacents car : |
Les angles xHt et xHw ne sont pas adjacents car ,
|
- ils ont le même sommet B ;
- ils ont un côté commun [Bv) ;
- ils ont de part et d'autre de ce côté commun.
|
même s'ils ont bien le même sommet H et un côté commun [Hx),
Il ne sont pas de part et d'autre de ce côté. |
|
| |
Définition :
Dire que deux angles sont opposés par le sommet signifie que ces deux angles sont symétriques par rapport à leur sommet.
|
|
|
| |
Exemple :
 |
 |
| |
|
|
 |
|
 |
|
 |
|
 |
| Les angles xFy et uFt sont opposés par les sommet |
Les angles wKz et uKx ne sont pas opposés par le |
| |
 |
|
 |
|
|
sommet car les côtés [Kz) et [Kx) ne sont pas |
| car xFy et uFt sont symétrique par rapport à F |
symétriqes par rapport à K. |
|
| |
Théorème :
Si deux angles sont opposés par le sommet
Alors ils sont égaux
|
|
| |
II - Angles alternes internes et angles correspondants |
|
| |
Définition :
Soit deux droites (d) et (d') coupées par sécante.
Dire que deux angles sont alternes internes signifie que :
- ils n'ont pas le même sommet ;
- ils sont de part et d'autre de la sécante ;
- ils sont à l'intérieur de la bande délimitée par les droites (d) et (d')
|
|
|
| |
Exemple :
Les deux angles vert et jaune, formés par
les droites (d) et (d') coupées par la
sécante (MN), sont alternes internes |
 |
|
|
| |
Définition :
Soit deux droites (d) et (d') coupées par sécante.
Dire que deux angles sont correspondants signifie que :
- ils n'ont pas le même sommet ;
- ils sont du même côté de la sécante ;
- l'un est à l'intérieur de la bande délimitée par les droites (d) et (d'), l'autre est à l'extérieur.
|
|
|
| |
Exemple :
Les deux angles vert et bleu, formés par
les droites (d) et (d') coupées par la
sécante (MN) sont correspondants. |
 |
|
|
| |
Théorème :
Si deux angles alternes internes sont formés par des droites parallèles
Alors ces deux angles sont égaux.
|
|
Ici on va encore avoir deux théorèmes réciproques, il faudra donc faire attention aux conditions d'utilisation et à la question pour ne pas se tromper de théorème. |
| |
Exemple : Démontrer que les angles en bleu sont égaux
 |
conditions d'utilisation |
conclusion |
- Deux droites parallèles coupées par une sécante
- Deux angles alternes internes
|
Les deux angles alternes internes sont égaux |
|
| |
Théorème :
Si deux angles alternes internes sont égaux
Alors ils sont formés par deux droites parallèles.
|
|
|
| |
Exemple : Démontrer que les droites coupées par la sécante sont parallèles
 |
conditions d'utilisation |
conclusion |
- Deux droites coupées par une sécante
- Deux angles alternes internes égaux
|
Les droites coupées par la sécante sont parallèles |
|
|
| |
Théorème :
Si deux angles correspondants sont formés par des droites parallèles
Alors ces deux angles sont égaux.
|
|
On a les même théorèmes que pour les angles alternes internes |
| |
Exemple : Démontrer que les angles en vert sont égaux
 |
conditions d'utilisation |
conclusion |
- Deux droites parallèles coupées par une sécante
- Deux angles correspondants
|
Les deux angles correspondants sont égaux |
|
|
| |
Théorème :
Si deux angles correspondants sont égaux
Alors ils sont formés par deux droites parallèles.
|
|
|
| |
Exemple : Démontrer que les droites coupées par la sécante sont parallèles
 |
conditions d'utilisation |
conclusion |
- Deux droites coupées par une sécante
- Deux angles correspondants égaux
|
Les droites coupées par la sécante sont parallèles |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les angles |
|
| |
|
Opérations sur les nombres en écriture fractionnaire |
| |
I - Somme ou différence de deux fractions |
|
| |
Théorème :
La somme (ou la différence) de deux nombres en écriture fractionnaire de même dénominateur est un nombre en écriture fractionnaire :
- son dénominateur est le même que celui des deux nombres.
- son numérateur est égal à la somme (ou à la différence) des numérateurs des deux nombres.
|
|
C'est la seule chose un peu particulière à retenir sur les fractions, alors un petit effort... |
| |
Formule :
|
|
| |
Exemples :
| 4 |
+ |
2 |
= |
4 + 2 |
= |
6 |
| 7 |
7 |
7 |
7 |
|
|
| |
La vraie question que vous devez surement vous poser maintenant est : mais qu'est-ce qu'on doit faire si jamais les fractions n'ont pas le même dénominateur, la réponse est simple : d'abord regarder par dessus l'épaule de son voisin .... discretement
puis se souvenir du chapitre précédent : il existe une infinité de façon d'écrire une fraction
parmis cette infinité, a nous de trouver celle qui nous permettra de faire le calcul.
| 1 |
+ |
5 |
Pour effectuer ce calcul, il faut passer par une première étape : mettre au même dénominateur. |
| 3 |
12 |
| 1 x 4 |
+ |
5 |
Il faut donc trouver comment passer de 3 à 12, c'est relativement facile 3 x 4 =12, on multiplie donc le numérateur et le dénominateur par 4
|
| 3 x 4 |
12 |
| 4 |
+ |
5 |
On peut maintenant appliquer le théorème précédent |
| 12 |
12 |
| 9 |
|
|
|
| 12 |
|
|
|
|
| |
II - Produit de deux fractions |
|
| |
Théorème :
Le produit de deux nombres en écriture fractionnaire est un nombre en écriture fractionnaire :
- son dénominateur est égal au produit des dénominateurs des deux nombres..
- son numérateur est égal au produit des numérateurs des deux nombres.
|
|
C'est beaucoup plus facile que pour les additions.... |
| |
Formule :
|
|
| |
Exemple :
| 2 |
x |
7 |
= |
2 x 7 |
= |
14 |
| 3 |
5 |
3 x 5 |
15 |
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les fractions |
|
| |
|
Parallélogrammes particuliers |
| |
I - Le rectangle |
|
| |
Théorème :
Si un parallélogramme a deux côtés consécutifs perpendiculaire
Alors c'est un rectangle
|
|
Vous pouvez retrouver la définition du rectangle dans le cours de 6ème |
| |
Exemple :
 |
ABCD est un rectangle |
|
|
| |
Théorème :
Si un parallélogramme a ses diagonales qui ont la même longueur
Alors c'est un rectangle
|
|
| |
Exemple :
 |
EFGH est un rectangle |
|
| |
II - Le losange |
|
| |
Théorème :
Si un parallélogramme a deux côtés consécutifs égaux
Alors c'est un losange
|
|
|
| |
Exemple :
 |
ALEX est un losange |
|
|
| |
Théorème :
Si un parallélogramme a ses diagonales perpendiculaires
Alors c'est un losange
|
|
|
| |
Exemple :
 |
PUFE est un losange |
|
|
| |
III - Le carré |
| |
Théorème :
Si un rectangle a deux côtés consécutifs égaux
Alors c'est un carré
|
Théorème :
Si un losange a deux côtés consécutifs peroendiculaire
Alors c'est un carré
|
|
|
| |
Exemple :
 |
BIDU est un carré |
|
|
| |
Théorème :
Si un parallélogramme a ses diagonales perpendiculaires et de même longueur
Alors c'est un carré
|
|
|
| |
Exemple :
 |
LANO est un carré |
|
|
| |
IV - Tableau récapitulatif : |
|
Ce tableau présente les propriétés à connaître pour chaque figure :
| Figures |
Propriétés des côtés |
Propriétés des diagonales |
| Parallélogramme |
 |
- côtés opposés parallèles
- côtés opposés égaux |
 |
elles se coupent en leur milieu |
| Rectangle |
 |
- côtés consécutifs perpendiculaires
- côtés opposés parallèles
- côtés opposés égaux
|
 |
- elles se coupent en leur milieu
- elles ont la même mesure |
| Losange |
 |
- côtés consécutifs égaux
- côtés opposés parallèles
- côtés opposés égaux |
 |
- elles se coupent en leur milieu
- elles sont perpendiculaires |
| Carré |
 |
- côtés consécutifs égaux et perpendiculaire
- côtés opposés parallèles
- côtés opposés égaux |
 |
- elles se coupent en leur milieu
- elles ont le même mesure
- elles sont perpendiculaires |
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les parallélogrammes particuliers |
|
| |
|
Echelle, mouvement uniforme |
| |
I - Echelle |
|
| |
Définition :
- Dire qu'une reproduction d'un objet est une représentation "à l'échelle" de cet objet signifie qu'il y a proportionnalité entre les longueurs de l'objetet celles de la reproduction.
- On appelle "échelle" le coefficient de proportionnalité qui permet de passer des longueurs de l'objet aux longueurs de la reproduction, exprimées dans la même unité.
| Echelle = |
Longueur sur la reproduction |
| Longueur sur l'objet |
|
|
|
| |
Vocabulaire :
La reproduction s'appelle une réduction lorsque l'échelle est inférieur à 1.
La reproduction s'appelle un agrandissement lorsque l'échelle est supérieur à 1.
|
|
| |
Exemple :
 |
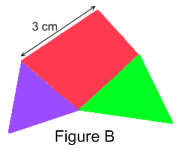 |
| La figure B est une représentation à l'échelle |
3 |
de la figure A. |
Dire que l'échelle est |
3 |
| 4 |
4 |
signifie que 3 cm sur la reproduction (figure B) représente 4 cm sur la figure originale (figure A)
La figure B est une réduction de la figure A. |
|
| |
II - Mouvement uniforme |
|
| |
|
| |
Définitions :
Dire qu'un mouvement est uniforme signifie qu'il y a proportionnalité entre la durée du trajet et la vitesse parcourue.
Dans un mouvement uniforme la vitesse est constante et cette vitesse est le coefficient de proportionnalité qui permet de passer de la duréee à la distance.
|
|
|
| |
Exemple :
| Durée (en h) |
2 |
2,5 |
5 |
| Distance (en Km) |
140 |
175 |
350 |
|
| 140 |
= 70 |
| 2 |
| 175 |
= 70 |
| 2,5 |
| 350 |
= 70 |
| 5 |
Il y a proportionnalité entre la distance et la durée.
Le mouvement est uniforme et la vitesse est 70 Km/h |
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec la proportionnalité |
|
| |
|
Aire |
| |
I - Aire d'un triangle |
|
| |
Propriété :
L'aire d'un triangle est égale à la moitié du produit d'un de ses côtés
par la hauteur relative à se côté.
|
|
Personnellement, je n'ai jamais compris pourquoi certains trouvaient ça dur, il suffit d'apprendre la formule et de l'appliquer... bêtement. |
| |
Figures à repérer :
|
|
| |
II - Aire d'un parallélogramme |
|
| |
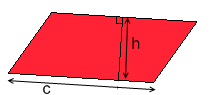
Propriété :
L'aire d'un parallélogramme est égale au produit d'un de ses côtés
par la hauteur relative à se côté.
|
|
|
| |
Figures à repérer :
|
|
| |
II - Aire d'un disque |
|
| |
Propriété :
L'aire d'un disque est égale au produit du nombre Pi ( P ) par le carré du rayon du disque
A = P x r |
|
|
|
| |
Exemple :
 |
A = P x 4 = 16 P cm = 16 P cm
la valeur approchée est : 16 x 3,14 = 50,24 cm
|
|
|
|
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les aires |
|
| |
|
Exploitation de données |
| |
I - Définition |
|
| |
Définition :
Lorsque l'on mène une enquête, on s'intéresse à une population d'individus (élèves d'une classe, pays de l'union européene, animaux d'une région ....) et on en étudie une propriété commune appelé un caractère ( taille des élèves, langue officielle, régime alimentaire...)
|
|
|
| |
Exemple :
Dans une classe de 5ème de 30 élèves, on a demandé à chaque élève le nombre de ses frères et soeurs.
Voici leur réponse :
| 1 |
2 |
0 |
1 |
1 |
3 |
2 |
4 |
1 |
1 |
2 |
0 |
2 |
6 |
1 |
| 7 |
2 |
1 |
3 |
1 |
0 |
5 |
2 |
1 |
2 |
1 |
1 |
3 |
2 |
1 |
La population d'individus étudiés est une classe de 5ème.
Le caractère étudié est le nombre de frères et soeurs
|
|
| |
Définition :
Pour un caractère donné, on appelle effectif d'une valeur le nombre de fois où cette valeur apparaît.
Le nombre d'individus de la population étudiée est appelé l'effectif total.
|
|
|
| |
Exemple :
Pour notre classe de 5ème, l'effectif total est 30.
Les valeurs du caractère sont : 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7
Dans cette classe, 12 élèves ont 1 frère ou une soeur.
L'effectif de la valeur "1" est 12.
|
|
| |
Définition :
Pour un caractère donné, on appelle fréquence d'une valeur quotient de l'effectif de cette valeur par l'effectif totale.
c'est donc la proportion de cette valeur par rapport à l'effectif totall.
|
|
Pour la fréquence, il suffit de se dire la valeur apparaît "un nombre de fois" SUR combien en tout. |
| |
Exemple :
Pour notre classe de 5ème, l'effectif total est 30.
| La fréquence de la valeur "1" est |
12 |
qui peut s'écrire 0,4 ou 40 % |
| 30 |
| La fréquence de chaque valeur peut être présentée dans un tableau : |
| Nombre de frères et soeurs |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Effectif |
3 |
12 |
8 |
3 |
1 |
1 |
1 |
1 |
| Fréquence |
|
|
|
|
|
|
|
|
|
|
|
| |
Remarques :
- La fréquence d'une valeur est toujours comprise entre 0 et 1.
- La somme des fréquences (ou fréquences totales) est toujours égale à 1.
|
Ce qui fournit un moyen de vérification très rapide |
| |
|
|
| |
II - Diagrammes |
Il faut comprendre qu'on n'utilise pas les même diagramme suivant le caractère et ce qu'on veut en faire. |
| |
a) Diagramme en barres
|
| |
Lorsque le caractère étudié n'est pas un nombre (caractère qualitatif), ses valeurs peuvent être représentées à l'aide d'un diagramme en barres.
|
| |
Exemple :
| On demande à des élèves de 5ème "que buvez-vous le plus ?", le tableau ci-dessous présente les résultats : |
| Boissons |
Jus de fruits |
Soda |
Lait |
Eau |
Autres |
| Effectif |
24 |
38 |
13 |
31 |
6 |
|
L'effectif total est obtenu par le calcul : 24 + 38 + 13 + 31 + 6 = 112
Les valeurs du caractère sont : jus de fruits ; soda ; lait ; eau et autres |
 |
|
|
| |
b) Diagramme en bâton
|
|
| |
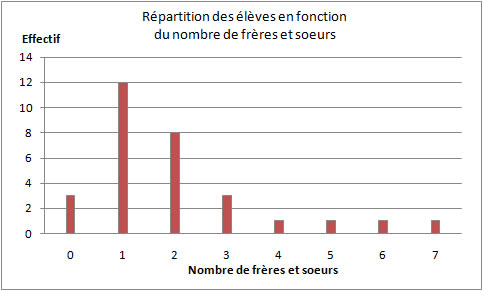
Lorsque le caractère étudié est un nombre (caractère quantitatif), ses valeurs peuvent être représentées à l'aide d'un diagramme en bâtons.
|
|
| |
Exemple :
| En utilisant le premier exemple, on a le tableau suivant : |
| Nombre de frères et soeurs |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Effectif |
3 |
12 |
8 |
3 |
1 |
1 |
1 |
1 |
|
 |
|
|
| |
c) Diagramme circulaire |
|
| |
Propriété :
Pour un diagramme circuaire, les angles des secteurs sont proportionnels aux effectif de chaque valeur.
|
|
|
| |
| pour réussir à tracer le diagramme circulaire, on va rajouter l'effectif total, ce qui nous permettra de travailler avec un angle connu : le tour du cercle fait 360° |
| Boissons |
Jus de fruits |
Soda |
Lait |
Eau |
Autres |
Total |
| Effectif |
24 |
38 |
13 |
31 |
6 |
112 |
| Angle |
77 |
122 |
42 |
100 |
19 |
360 |
|
| Le coefficient de proportionnalité est |
360 |
, ce qui nous permet de trouver les angles |
| 112 |
 |
|
|
| |
III - Regroupement en classe |
|
| |
Lorsque les données sont nombreuses, on peut les regrouper en classes pour faciliter leur lecture. |
|
| |
Exemple :
| Voici les tailles en cm de quelques joueurs de volley-bal : |
| 194 |
195 |
188 |
194 |
190 |
185 |
193 |
198 |
189 |
200 |
187 |
190 |
192 |
192 |
191 |
190 |
| 195 |
197 |
186 |
189 |
194 |
194 |
200 |
196 |
192 |
185 |
182 |
195 |
195 |
195 |
191 |
190 |
| 191 |
185 |
198 |
189 |
195 |
191 |
200 |
188 |
190 |
198 |
195 |
195 |
185 |
190 |
190 |
190 |
|
| La population d'individus étudiée est un groupe de joueurs de volley-ball. Son effectif total est 48. |
Les valeurs du caractère sont des nombres compris entre 183 et 200
Ces tailles étant très diverses, il est préférable de les regrouper par classes d'amplitude 3 cm : |
| Taille t (en cm) |
182  t < 185 t < 185 |
185  t < 188 t < 188 |
188  t < 191 t < 191 |
191  t < 194 t < 194 |
194  t < 197 t < 197 |
197  t < 200 t < 200 |
200  t < 203 t < 203 |
| Effectif |
1 |
6 |
13 |
8 |
13 |
4 |
3 |
|
 |
|
|
|
| |
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec les statistiques |
|
| |
|
Géométrie dans l'espace |
| |
I - Prisme droit |
|
| |
Définition :
Un prisme droit est le solide qui possède :
- deux bases parallèles et superposables qui sont toujours des polygones (triangle, quadrilatère, pentagone ......)
- des faces latérales perpendiculaires aux bases qui sont toujours des rectangles.
|
|
|
| |
Exemple :
 |
| Ce prisme a comme base un pentagone. |
Un pavé droit est un prisme droit qui a comme base un rectangle.
Un cube est un prisme droit qui a comme base un carré. |
|
|
| |
Patron d'un prisme droit : |
|
| |
Exemple :
|
|
| |
II - Cylindre de révolution |
|
| |
Définition :
Un cylindre de révolution est le solide qui possède :
- deux bases parallèles et superposables qui sont toujours des disques
- une surface latérale courbe qui mise à plat est un rectangle.
Ce rectangle a pour dimension la hauteur du cylindre et le périmètre du disque.
|
|
|
| |
Exemple :
|
|
| |
Patron d'un cylindre de révolution : |
|
| |
Exemple :
|
|
| |
III - Volume d'un prisme droit et d'un cylindre de révolution |
|
| |
Définition :
Le volume d'un prisme droit ou d'un cylindre de révolution s'obtient par la formule :
V = Aire de la base x Hauteur
|
|
|
| |
Remarque : Avant de pouvoir calculer le volume du solide, il va falloir calculer l'aire de sa base et pour ça il faut donc connaître ses formules d'aires.....
Exemple :
|
|
|
| |
|
 |
|
Vous trouverez ici des liens
vers des exercices en relation avec la géométrie dans l'espace |
|
Le programme de 5ème est maintenant terminé, à bientôt pour le programme de quatrième ...... |